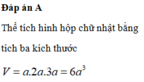Các câu hỏi tương tự
Gọi a, b, c lần lượt là ba kích thước của một khối hộp chữ nhật (H) và V là thể tích của khối hộp chữ nhật (H). Khi đó V được tính bởi công thức:
Đọc tiếp
Gọi a, b, c lần lượt là ba kích thước của một khối hộp chữ nhật (H) và V là thể tích của khối hộp chữ nhật (H). Khi đó V được tính bởi công thức:
![]()
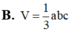
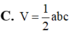
![]()
Hình hộp chữ nhật có 3 kích thước là 2 , 3 , 6 có thể tích là:
A . 1
B . 2
C . 6
D . 6
Khối hộp chữ nhật có 3 cạnh xuất phát từ một đỉnh lần lượt có độ dài a, b, c. Thể tích khối hộp chữ nhật là ? A.
1
3
a
b
c
B. abc. C.
1
6
a
b
c
D.
4
3
a
b
c
Đọc tiếp
Khối hộp chữ nhật có 3 cạnh xuất phát từ một đỉnh lần lượt có độ dài a, b, c. Thể tích khối hộp chữ nhật là ?
A. 1 3 a b c
B. abc.
C. 1 6 a b c
D. 4 3 a b c
Cho hình hộp chữ nhật
A
B
C
D
.
A
1
B
1
C
1
D
1
có ba kích thước AB a, AD 2a,
A
A
1
3
a
. Khoảng cách từ A đến mặt phẳng
(
A
1
B...
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A 1 B 1 C 1 D 1 có ba kích thước AB =a, AD = 2a, A A 1 = 3 a . Khoảng cách từ A đến mặt phẳng ( A 1 B D ) bằng bao nhiêu?
A. a
B. 7 a 6
C. 5 a 7
D. 6 a 7
Nếu ba kích thước của một khối hộp chữ nhật tăng lên 3 lần thì thể tích của nó tăng lên bao nhiêu lần?
A. 27 lần
B. 9 lần
C. 18 lần
D. 3 lần
Thể tích của khối hộp chữ nhật có độ dài các cạnh bằng a, b, c là A.
1
6
abc B.
1
2
abc C. abc D.
1
3
abc
Đọc tiếp
Thể tích của khối hộp chữ nhật có độ dài các cạnh bằng a, b, c là
A. 1 6 abc
B. 1 2 abc
C. abc
D. 1 3 abc
Cho hình hộp chữ nhật ABCD. A’B’C’D’có AB a, BC 2a, AA’ a. Lấy điểm I trên cạnh AD sao cho AI 3 ID. Tính thể tích của khối chop B’. IAC.
Đọc tiếp
Cho hình hộp chữ nhật ABCD. A’B’C’D’có AB = a, BC = 2a, AA’ = a. Lấy điểm I trên cạnh AD sao cho AI = 3 ID. Tính thể tích của khối chop B’. IAC.
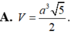
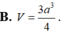
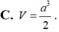
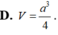
Một xưởng sản xuất những thùng bằng kẽm hình hộp chữ nhật không có nắp và có các kích thước x, y, z (dm). Biết tỉ số hai cạnh đáy là x : y 1 : 3 thể tích của khối hộp bằng 18 lít. Để tốn ít vật liệu nhất thì bộ số x, y, z là A. x 2, y 6, z
3
2
B. x 1, y 3, z 6 C. x
3
2
,
y
9
2
,...
Đọc tiếp
Một xưởng sản xuất những thùng bằng kẽm hình hộp chữ nhật không có nắp và có các kích thước x, y, z (dm). Biết tỉ số hai cạnh đáy là x : y = 1 : 3 thể tích của khối hộp bằng 18 lít. Để tốn ít vật liệu nhất thì bộ số x, y, z là
A. x= 2, y = 6, z = 3 2
B. x =1, y = 3, z =6
C. x= 3 2 , y = 9 2 , z = 3 2
D.x= 1 2 , y= 3 2 , z= 24
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có các kích thước là AB 2, AD 3, AA’ 4. Gọi (N) là hình nón có đỉnh là tâm của mặt ABB’A’ và đường tròn đáy là đường tròn ngoại tiếp hình chữ nhật CDD’C’. Tính thể tích V của hình nón (N). A.
13
3
π
B. 5
π
C. 8
π
D.
25
6
π
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có các kích thước là AB= 2, AD= 3, AA’= 4. Gọi (N) là hình nón có đỉnh là tâm của mặt ABB’A’ và đường tròn đáy là đường tròn ngoại tiếp hình chữ nhật CDD’C’. Tính thể tích V của hình nón (N).
A. 13 3 π
B. 5 π
C. 8 π
D. 25 6 π