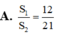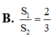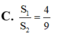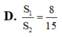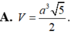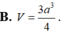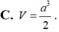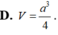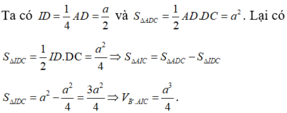Các câu hỏi tương tự
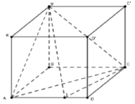
Cho hình hộp chữ nhật ABCD.ABCD có ABa, AA2a Biết thể tích hình cầu ngoại tiếp tứ diện ABCD là
9
π
a
3
2
Tính thể tích V của hình hộp chữ nhật ABCD.ABCD.
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=a, AA'=2a Biết thể tích hình cầu ngoại tiếp tứ diện ABCD' là 9 π a 3 2 Tính thể tích V của hình hộp chữ nhật ABCD.A'B'C'D'.
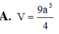
![]()
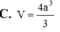
![]()
Cho hình hộp chữ nhật ABCD. A’B’C’D’có thể tích bằng 48 Tính thể tích phần chung của hai khối chóp AB’CD’và A’BC’D.
A. 10
B. 12
C. 8
D. 6
Cho hình hộp ABCD A B C D . A'B C'D ' có :
AB=1, AD=2, A A'=3. Góc BAD =120 độ, BAA= 60 độ , DAA=60 độ . Gọi I là giao điểm của BC' và BC' . 1) Tính các tích sau AB .AD ,AB. AA' ,AD. AA'. 2) Tính AI AC . 3) Tính AI . 4) Tính góc giữa AI và AC'.Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB2a, BCa. Các cạnh bên của hình chóp bằng nhau và bằng
a
2
. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. K là điểm trên cạnh AD sao cho KD2KA. Tính khoảng cách giữa hai đường thẳng MN và SK.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=2a, BC=a. Các cạnh bên của hình chóp bằng nhau và bằng a 2 . Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. K là điểm trên cạnh AD sao cho KD=2KA. Tính khoảng cách giữa hai đường thẳng MN và SK.
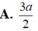
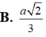
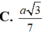
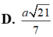
Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB2a, AD3a. Cạnh bên SA vuông góc với đáy (ABCD), SAa. Tính thể tích V của khối chóp S.ABCD.
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB=2a, AD=3a. Cạnh bên SA vuông góc với đáy (ABCD), SA=a. Tính thể tích V của khối chóp S.ABCD.
![]()
![]()
![]()
![]()
Cho hình hộp chữ nhật ABCD. A’B’C’D’ có AB a, AD 2a, AA’ a. Gọi M là điểm trên đoạn AD với
A
D
M
D
. Gọi x là độ dài khoảng cách giữa hai đường thẳng AD, B C và y là độ dài khoảng cách từ M đến mặt phẳng (AB’C). Tính giá trị xy A.
5
a
5
3
B. ...
Đọc tiếp
Cho hình hộp chữ nhật ABCD. A’B’C’D’ có AB =a, AD = 2a, AA’ =a. Gọi M là điểm trên đoạn AD với A D M D . Gọi x là độ dài khoảng cách giữa hai đường thẳng AD', B 'C và y là độ dài khoảng cách từ M đến mặt phẳng (AB’C). Tính giá trị xy
A. 5 a 5 3
B. a 2 2
C. 3 a 2 4
D. 3 a 2 2
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB a, AD 2a, AA’ 3a Gọi M, N, P lần lượt là trung điểm của BC, C’D’ và DD’. Tính khoảng cách từ A đến mp (MNP). A.
15
22
a
B.
9
11
a
C.
3
4
a
D.
15
11
a
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, AD =2a, AA’= 3a Gọi M, N, P lần lượt là trung điểm của BC, C’D’ và DD’. Tính khoảng cách từ A đến mp (MNP).
A. 15 22 a
B. 9 11 a
C. 3 4 a
D. 15 11 a
Cho khối tứ diện ABCD có thể tích
V
0
. Dựng hình hộp sao cho AB, AC, AD là ba cạnh của hình hộp. Tính thể tích V của khối hộp đó.
Đọc tiếp
Cho khối tứ diện ABCD có thể tích V 0 . Dựng hình hộp sao cho AB, AC, AD là ba cạnh của hình hộp. Tính thể tích V của khối hộp đó.
![]()
![]()
![]()
![]()
Cho hình chữ nhật ABCD có AB2a, BC3a. Gọi M, N lần lượt là các điểm trên cạnh AD, BC sao cho MA2MD, NB2NC Khi quay quanh AB, các đường gấp khúc AMNB, ADCB sinh ra các hình trụ có diện tích toàn phần
S
1
S
2
Tính tỉ số
S
1
S
2
là:
Đọc tiếp
Cho hình chữ nhật ABCD có AB=2a, BC=3a. Gọi M, N lần lượt là các điểm trên cạnh AD, BC sao cho MA=2MD, NB=2NC Khi quay quanh AB, các đường gấp khúc AMNB, ADCB sinh ra các hình trụ có diện tích toàn phần S 1 S 2 Tính tỉ số S 1 S 2 là: