Các câu hỏi tương tự
Cho hình hộp chữ nhật ABCD. A’B’C’D’có AB a, BC 2a, AA’ a. Lấy điểm I trên cạnh AD sao cho AI 3 ID. Tính thể tích của khối chop B’. IAC.
Đọc tiếp
Cho hình hộp chữ nhật ABCD. A’B’C’D’có AB = a, BC = 2a, AA’ = a. Lấy điểm I trên cạnh AD sao cho AI = 3 ID. Tính thể tích của khối chop B’. IAC.
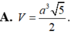
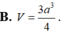
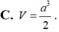
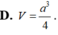
Cho hình hộp chữ nhật ABCD. A’B’C’D’ có thể tích bằng 1 và G là trọng tâm tam giác BCD’ Thể tích V của khối chóp G. ABC’ là A.
V
1
3
B.
V
1
6
C.
V
1
12
D.
V
...
Đọc tiếp
Cho hình hộp chữ nhật ABCD. A’B’C’D’ có thể tích bằng 1 và G là trọng tâm tam giác BCD’ Thể tích V của khối chóp G. ABC’ là
A. V = 1 3
B. V = 1 6
C. V = 1 12
D. V = 1 18
Cho hình hộp ABCD. A’B’C’D’ gọi O là giao điểm của AC và BD. Tính tỉ số thể tích của khối chóp O. ABC và khối hộp ABCD. A’B’C’D’ điểm của AC và BD. Tính tỉ số thể tích của khối chóp O. ABC và khối hộp ABCD. A’B’C’D’ A.
1
4
B.
1
3
C.
1
6
D.
1
12
Đọc tiếp
Cho hình hộp ABCD. A’B’C’D’ gọi O là giao điểm của AC và BD. Tính tỉ số thể tích của khối chóp O. ABC và khối hộp ABCD. A’B’C’D’ điểm của AC và BD. Tính tỉ số thể tích của khối chóp O. ABC và khối hộp ABCD. A’B’C’D’
A. 1 4
B. 1 3
C. 1 6
D. 1 12
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Biết diện tích đáy bằng m, thể tích V của khối chóp S.ABCD là A.
V
1
3
m
SA B.
V
1
3
m
SB C.
V
1...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Biết diện tích đáy bằng m, thể tích V của khối chóp S.ABCD là
A. V = 1 3 m SA
B. V = 1 3 m SB
C. V = 1 3 m SC
D. V = 1 3 m SD
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA vuông góc với mặt đáy (ABCD) Thể tích V của khối chóp S.ABCD bằng
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật 
và SA vuông góc với mặt đáy (ABCD) Thể tích V của khối chóp S.ABCD bằng
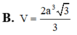
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, và SA vuông góc với mặt đáy (ABCD). Thể tích V của khối chóp S.ABCD bằng
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, 
và SA vuông góc với mặt đáy (ABCD). Thể tích V của khối chóp S.ABCD bằng
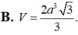
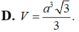
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 48. Gọi M,N lần lượt là điểm thuộc các cạnh AB, CD sao cho MAMB, NC 2ND . Tính thể tích V của khối chóp S.MBCN A. V8 B. V20 C. V 28 D. V40
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 48. Gọi M,N lần lượt là điểm thuộc các cạnh AB, CD sao cho MA=MB, NC =2ND . Tính thể tích V của khối chóp S.MBCN
A. V=8
B. V=20
C. V= 28
D. V=40
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, hai mặt phẳng (SAC) và (SBD) cùng vuông góc với đáy, ABa, AD2a. Khoảng cách giữa hai đường thẳng AB và SD bằng
a
3
Thể tích khối chóp S.ABCD bằng
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, hai mặt phẳng (SAC) và (SBD) cùng vuông góc với đáy, AB=a, AD=2a. Khoảng cách giữa hai đường thẳng AB và SD bằng a 3 Thể tích khối chóp S.ABCD bằng
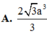
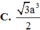
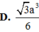
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành có thể tích là V. Gọi M là một điểm trên cạnh AB sao cho
M
A
A
B
x
, 0 x 1. . Biết rằng mặt phẳng
α
qua M và song song với (SBC) chia khối chóp S. ABCD thành hai phần trong đó phần chứa điểm A thể tích bằng
4
27
V...
Đọc tiếp
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành có thể tích là V. Gọi M là một điểm trên cạnh AB sao cho M A A B = x , 0< x < 1. . Biết rằng mặt phẳng α qua M và song song với (SBC) chia khối chóp S. ABCD thành hai phần trong đó phần chứa điểm A thể tích bằng 4 27 V . Tính giá trị của biểu thức 1 - x 1 + x
A. 1 2
B. 1 5
C. 1 3
D. 3 5