Điều kiện: x > 0
Ta có đẳng thức ![]()
Do đó bất phương trình ![]()
![]()
![]()
Chọn A.
Điều kiện: x > 0
Ta có đẳng thức ![]()
Do đó bất phương trình ![]()
![]()
![]()
Chọn A.
Cho hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e , ( a , b , c , d , e ∈ ℝ ) Hàm y=f'(x) có bảng xét dấu như sau:
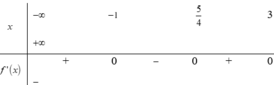
Số nghiệm của phương trình f(x)=e là
A. 1
B. 0
C. 2
D. 3
Biết rằng tập nghiệm S của bất phương trình log - x 2 + 100 x - 2400 < 2 có dạng S = a ; b \ x ∘ . Giá trị của a + b - x ∘ bằng:
A. 150.
B. 100.
C. 30.
D. 50.
Cho tham số thực a. Biết phương trình e x − e − x = 2 cos a x có 5 nghiệm thực phân biệt. Hỏi phương trình e x − e − x = 2 cos a x + 4 có bao nhiêu nghiệm thực phân biệt?
A. 5.
B. 6.
C. 10.
D. 11.
Cho hàm số f ( x ) = l n ( x 2 - 2 x + 3 ) . Tập nghiệm của bất phương trình f'(x)>0 là
A. ( 2 ; + ∞ ) .
B. ( - 1 ; + ∞ ) .
C. ( - 2 ; + ∞ ) .
D. ( 1 ; + ∞ ) .
Biết rằng phương trình a x 4 + b x 3 + c x 2 + d x + e = 0 a , b , d , e ∈ ℝ , a ≠ 0 , b ≠ 0 có 4 nghiệm thực phân biệt. Hỏi phương trình sau có bao nhiêu nghiệm thực?
4
a
x
3
+
3
b
x
2
+
2
c
x
+
d
2
−
2
6
a
x
2
+
3
b
x
+
c
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
e
=
0
A. 0
B. 2
C. 4
D. 6
Tập nghiệm của bất phương trình 2 x 2 − 4 − 1 . ln ( x 2 ) < 0 là
A. S = [ 1 ; 2 ] .
B. S = { 1 ; 2 } .
C. S = ( 1 ; 2 ) .
D. S = ( − 2 ; − 1 ) ∪ ( 1 ; 2 ) .
\(\int\limits^{ln\sqrt{3}}_0\frac{dx}{e^x+e^{-x}}\)
Nghiệm của bất phương trình e x + e - x < 5 2 là:
A. x < 1 2 hoặc x > 2
B. 1 2 < x < 2
C. -ln2 < x < ln2
D. x < -ln2 hoặc x > ln2
Kí hiệu F (x) là một nguyên hàm của hàm số f ( x ) = 1 e x + 1 , biết F 0 = - ln 2 . Tìm tập nghiệm S của phương trình F ( x ) + ln ( e x + 1 ) = 3 .
A. S = - 3 ; 3
B. S = 3
C. S = ∅
D. S = - 3