Các câu hỏi tương tự
Biết tập nghiệm S của bất phương trình log0,3( 4x2) ≥ log0,3( 12x-5) là một đoạn. Gọi m, M lần lượt là giá trị nhỏ nhất, lớn nhất của tập S. Mối liên hệ giữa m và M là A. M+ n 3 B.M+ n 2 C.M- n 3 D. M- n1
Đọc tiếp
Biết tập nghiệm S của bất phương trình log0,3( 4x2) ≥ log0,3( 12x-5) là một đoạn. Gọi m, M lần lượt là giá trị nhỏ nhất, lớn nhất của tập S. Mối liên hệ giữa m và M là
A. M+ n= 3
B.M+ n= 2
C.M- n= 3
D. M- n=1
Nghiệm của bất phương trình
log
2
3
x
-
2
0 là:A. x 1 B. x 1C. 0 x 1 D.
log
3
2
x 1
Đọc tiếp
Nghiệm của bất phương trình log 2 3 x - 2 < 0 là:
A. x > 1 B. x < 1
C. 0 < x < 1 D. log 3 2 < x < 1
Nghiệm của bất phương trình log 2 ( 3 x - 2 ) < 0 là:
A. x > 1 B. x < 1
C. 0 < x < 1 D. log 3 2 < x < 1
Tìm tập nghiệm của bất phương trình: 2 2 x 8 > 1
A. x > 3/2 B. x < 3/2
C. x > 2/3 D. x < 2/3
Tập nghiệm của bất phương trình
2
log
3
(
x
-
1
)
+
log
3
(
2
x
-
1
)
≤
2
là A. S (1; 2] B. S
(
-
1
2
;
2
)
C. [1; 2] D.
[...
Đọc tiếp
Tập nghiệm của bất phương trình 2 log 3 ( x - 1 ) + log 3 ( 2 x - 1 ) ≤ 2 là
A. S = (1; 2]
B. S = ( - 1 2 ; 2 )
C. [1; 2]
D. [ - 1 2 ; 2 ]
Biết tập nghiệm của bất phương trình x2- 6x + 2 + \(_{log_2\left(x^2-2x\right)+log_{\frac{1}{2}}\left(x-1\right)< 0}\) là khoảng ( 2 ; a + \(\sqrt{b}\)) với a, b là số tự nhiên. Giá trị của a + b bằng
Tập nghiệm của bất phương trình
2
x
+
2
(
x
+
1
)
≤
3
x
+
3
(
x
-
1
)
A.
x
∈
[...
Đọc tiếp
Tập nghiệm của bất phương trình 2 x + 2 ( x + 1 ) ≤ 3 x + 3 ( x - 1 )
A. x ∈ [ 2 ; + ∞ )
B. x ∈ 2 ; + ∞
C. x ∈ - ∞ ; 2
D. 2 ; + ∞
Tập nghiệm của bất phương trình
2
x
+
2
(
x
+
1
)
≤
3
x
+
3
(
x
-
...
Đọc tiếp
Tập nghiệm của bất phương trình 2 x + 2 ( x + 1 ) ≤ 3 x + 3 ( x - 1 )
A. x ∈ [ 2 ; + ∞ )
B. x ∈ 2 ; + ∞
C. x ∈ - ∞ ; 2
D. 2 ; + ∞
Tìm tập nghiệm của bất phương trình:
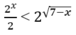
A. x < 3 B. x ≥ 1
C. 1 ≤ x < 3 D. x < 1