Đáp án A
Hướng dẫn giải
Đặt 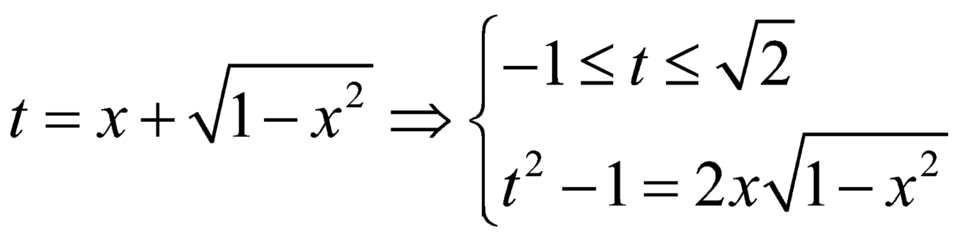
Khi đó: ![]()
![]() .
.
Xét hàm ![]()
![]() . Hàm số luôn đồng biến.
. Hàm số luôn đồng biến.
![]()
![]()
![]() .
.
Phương trình có nghiệm: 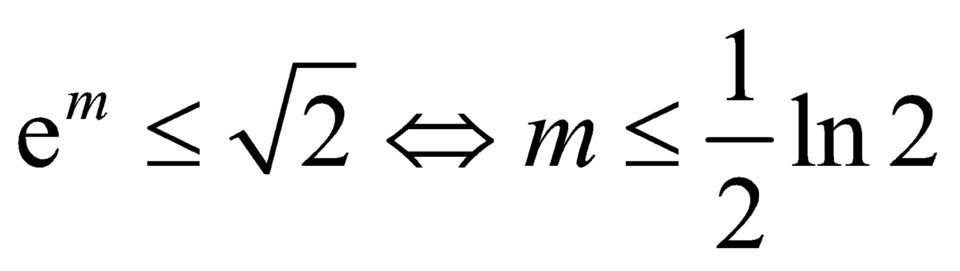 .
.
Đáp án A
Hướng dẫn giải
Đặt 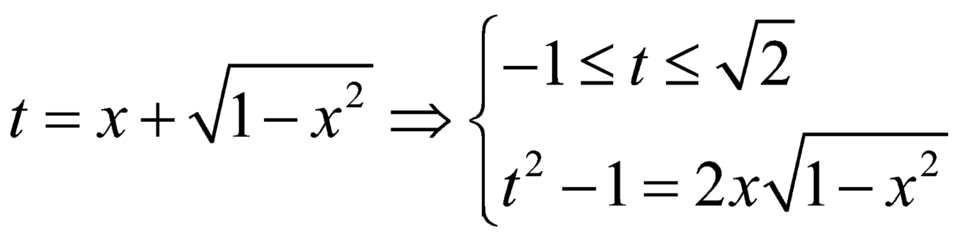
Khi đó: ![]()
![]() .
.
Xét hàm ![]()
![]() . Hàm số luôn đồng biến.
. Hàm số luôn đồng biến.
![]()
![]()
![]() .
.
Phương trình có nghiệm: 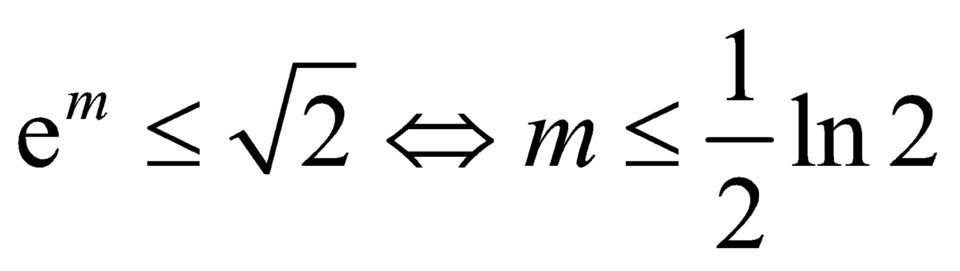 .
.
Cho phương trình m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0 . Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình đã cho có hai nghiệm thực x1, x2 thỏa 0 < x1 < 1 < x2
A. 2 ; + ∞
B. - 1 ; 2
C. - ∞ ; - 1
D. - ∞ ; - 1 ∪ 2 ; + ∞
Cho phương trình m . l n 2 ( x + 1 ) - ( x + 2 - m ) l n ( x + 1 ) - x - 2 = 0 (1). Tập hợp tất cả các giá trị của tham số m để phương trình (1) có hai nghiệm phân biệt thoả mãn 0 < x 1 < 2 < 4 < x 2 là khoảng . Khi đó a thuộc khoảng
![]()
![]()
![]()
![]()
Tìm tập hợp tất cả các giá trị của tham số m để phương trình 5 x + 2 - x - 5 m = 0 có nghiệm thực
![]()
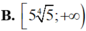
![]()
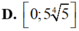
Tìm tất cả các giá trị thực của tham số m để phương trình log 2 5 x - 1 . log 4 2 . 5 x - 2 = m có nghiệm x ≥ 1
A. m ∈ (-∞;2)
B. m ∈ (2;+∞)
C. m ∈ (3;+∞)
D. m ∈ (-∞;3)
Cho hàm số y = ax 3 + bx 2 + cx + d với a ≠ 0 có hai hoành độ cực trị là x=1 và x=3. Tập hợp tất cả các giá trị của tham số m để phương trình f(x) = f(m) có đúng ba nghiệm phân biệt là:
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y = a x 3 + b x 2 + c x + d với a khác 0 có hai hoành độ cực trị là x=1 và x=3. Tập hợp tất cả các giá trị của tham số m để phương trình f(x) = f(m) có đúng ba nghiệm phân biệt là:
![]()
![]()
![]()
![]()
Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình x.2x = x(x - m +1) + m(2x - 1) có hai phần tử.Tìm số phần tử của A.
A. 1
B. Vô số
C. 3
D. 2
Tìm tất cả các giá trị thực của tham số m để bất phương trình log 2 5 x - 1 . log 2 2 . 5 x - 2 ≥ m có nghiệm x ≥ 1
A. m ≥ 6
B. m > 6
C. m ≤ 6
D. m < 6
Hình bên là đồ thị của hàm số y = x 3 - 3 x Tìm tất cả các giá trị thực của tham số m để phương trình 64 | x | 3 = ( x 2 + 1 ) 2 ( 12 | x | + m ( x 2 + 1 ) ) có nghiệm.
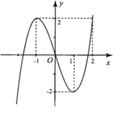
A.![]()
B. Với mọi m
C. ![]()
D. ![]()
Cho S là tập hợp các giá trị thực của tham số m để phương trình 2 - x + 1 - x = m + x - x 2 có hai nghiệm phân biệt. Tổng các số nguyên trong S bằng
A. 11.
B. 0.
C. 5.
D. 6.