Các câu hỏi tương tự
Tập hợp tất cả các giá trị thực của tham số thực m để hàm số y = l n ( x 2 + 1 ) - m x + 1 đồng biến trên R
A. [-1;1].
B. (-1;1)
C. (-∞;-1]
D.(- ∞;-1)
Cho hàm số
y
2
x
+
1
+
1
2
-
m
với m là tham số thực. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m trong khoảng (-50;50) để hàm số nghịch biến trên khoảng (-1;1). Số phần tử của tập hợp S là: A. 47 B. 48 C. 50 D. 49
Đọc tiếp
Cho hàm số y = 2 x + 1 + 1 2 - m với m là tham số thực. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m trong khoảng (-50;50) để hàm số nghịch biến trên khoảng (-1;1). Số phần tử của tập hợp S là:
A. 47
B. 48
C. 50
D. 49
Cho hàm số
y
2
x
+
1
+
1
2
x
-
m
với m là tham số thực. Gọi S là tập hợp tất cả c...
Đọc tiếp
Cho hàm số y = 2 x + 1 + 1 2 x - m với m là tham số thực. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m trong khoảng (–50;50) để hàm số ngịch biến trên (–1;1). Số phần tử của S là:
A. 49
B. 47
C. 48
D. 50
Tìm tất cả các giá trị thực của tham số m để trên
(
-
1
;
1
)
hàm số
y
m
x
+
6
2
x
+
m
+
1
nghịch biến A.
-
4
m
3
B....
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để trên ( - 1 ; 1 ) hàm số y = m x + 6 2 x + m + 1 nghịch biến
A. - 4 < m < 3
B. - 4 ≤ m < - 3 1 < m ≤ 3
C. 1 ≤ m < 4
D. - 4 < m ≤ - 3 1 ≤ m < 3
Tìm tất cả các giá trị thực của tham số m để hàm số
y
m
x
+
6
2
x
+
m
+
1
nghịch biến trên (-1;1)
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = m x + 6 2 x + m + 1 nghịch biến trên (-1;1)
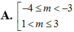
![]()
![]()
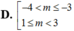
Tìm tập hợp S tất cả các giá trị của tham số thực m để hàm số
y
1
3
x
3
−
m
+
1
x
2
+
m
2
+
2
m
x
−
3
nghịch biến trên khoảng (-1;1). A. ...
Đọc tiếp
Tìm tập hợp S tất cả các giá trị của tham số thực m để hàm số y = 1 3 x 3 − m + 1 x 2 + m 2 + 2 m x − 3 nghịch biến trên khoảng (-1;1).
A. S = − 1 ; 0
B. S = ∅
C. S = − 1
D. S = 0 ; 1
Tập hợp S tất cả các giá trị của tham số thực m để hàm số sau nghịch biến trên khoảng (-1;1):
y
1
3
x
3
-
m
+
1
x
2
+
m
2
+
2
m
x
-
3
A.
S
∅
B.
S...
Đọc tiếp
Tập hợp S tất cả các giá trị của tham số thực m để hàm số sau nghịch biến trên khoảng (-1;1): y = 1 3 x 3 - m + 1 x 2 + m 2 + 2 m x - 3
A. S = ∅
B. S = 0 ; 1
C. S = - 1 ; 0
D. S = - 1
Tập hợp tất cả các giá trị thực của tham số m để hàm số
y
ln
x
2
+
1
−
m
x
+
1
đồng biến trên R là: A. [-1;1] B.
−
∞
;
−
1
C.
−
1
;...
Đọc tiếp
Tập hợp tất cả các giá trị thực của tham số m để hàm số y = ln x 2 + 1 − m x + 1 đồng biến trên R là:
A. [-1;1]
B. − ∞ ; − 1
C. − 1 ; 1
D. − ∞ ; − 1
Cho hàm số yf(x) xác định trên
R
∖
{
-
1
;
1
}
liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau.Tìm tập hợp tất cả các giá trị của tham số m sao cho phương trình f(x)m có đúng 1 nghiệm. A.
{
-
3
2
;
3
2
;
1
}
B....
Đọc tiếp
Cho hàm số y=f(x) xác định trên R ∖ { - 1 ; 1 } liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau.
Tìm tập hợp tất cả các giá trị của tham số m sao cho phương trình f(x)=m có đúng 1 nghiệm.
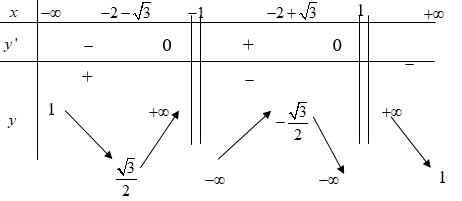
A. { - 3 2 ; 3 2 ; 1 }
B. { - 3 2 ; 3 2 }
C. { 1 }
D. ( 1 ; + ∞ )




