Đáp án C
Vì - 1 ≤ sin 2 x ≤ 1 ⇒ - 1 + 3 ≤ sin 2 x + 3 ≤ 1 + 3 ⇔ 2 ≤ y ≤ 4 . Vậy tập giá trị là [2;4]
Đáp án C
Vì - 1 ≤ sin 2 x ≤ 1 ⇒ - 1 + 3 ≤ sin 2 x + 3 ≤ 1 + 3 ⇔ 2 ≤ y ≤ 4 . Vậy tập giá trị là [2;4]
Cho hàm số y=f(x), xÎ[-2;3] có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn Î[-2;3]. Giá trị của S=M+m là
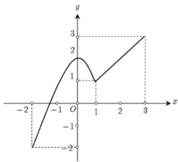
A. 6
B. 1
C. 5
D. 3
Cho hàm số y = f x , x ∈ - 2 ; 3 có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x trên đoạn - 2 ; 3 . Giá trị của S = M + m là:
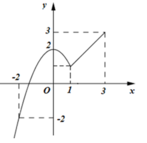
A. 6
B. 3
C. 5
D. 1
Cho hàm số y = f x , x ∈ - 2 ; 3 có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn - 2 ; 3 . Giá trị của biểu thức 2 m + log 9 M bằng
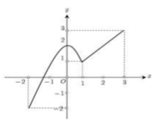
A. 1 8
B. 3 8
C. 3 4
D. 3 2
Gọi S là tập hợp các giá trị thực của tham số m làm cho hàm số y = 2 x 2 − 4 x + m x 2 − 2 x + 3 đồng biến trên khoảng (2;3). Khi đó tập S là
A. S = − ∞ ; 6 .
B. S = − ∞ ; 6 .
C. S = 2 ; 3 .
D. S = 6 ; + ∞ .
Cho hàm số y = x + 2 x - 1 . Giá trị m i n x ∈ 2 ; 3 y 2 + m a x x ∈ 2 ; 3 y 2 bằng
A. 16
B. -1
C. 0
D. 89 4
Giá trị lớn nhất của hàm số y = 2 mx + 1 m - x trên 2 ; 3 là - 1 3 khi m nhận giá trị bằng:
A. -5
B. 1
C. 0
D. -2
Cho hàm số y = − x 2 + 2 , khi x ≤ 1 x , k h i x > 1 . Tìm giá trị lớn nhất của hàm số trên đoạn − 2 ; 3
A. max − 2 ; 3 y = − 2
B. max − 2 ; 3 y = 2
C. max − 2 ; 3 y = 1
D. max − 2 ; 3 y = 3
Gọi T là tập hợp tất cả các giá trị của tham số m để hàm số y = m x + 1 x + m 2 có giá trị lớn nhất trên đoạn 2 ; 3 bằng 5 6 . Tính tổng của các phần tử trong T.
A. 17 5
B. 2
C. 6
D. 16 5
Cho hàm số y=f(x) có bảng biến thiên như sau:
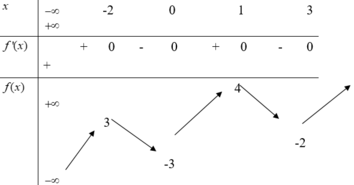
Tích của giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [-2;3] bằng
A. -6
B. -8
C. -12
D. -9
Tìm giá trị nhỏ nhất của hàm số y = 2 x + 1 1 − x trên đoạn 2 ; 3
A.1
B.-2
C.0
D.-5