Đáp án B
Đặt t = log 3 2 x + 1 thay vào PT log 3 2 x + log 3 2 x + 1 − 2 m − 1 = 0 1 phương trình đã cho trở thành t 2 + t − 2 m − 2 = 0 ⇔ t 2 + t − 2 = 2 m 2 . Để phương trình (1) có nghiệm trên đoạn 1 ; 3 3 thì PT (2) có nghiệm trên 1 ; 2 .
Xét hàm số f ' t = 2 t + 1 ⇒ f ' t = 0 ⇔ t = − 1 2 ta có BBT của f(t) như sau:
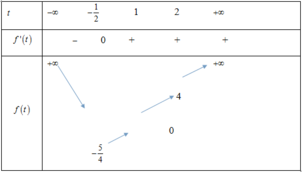
Qua BBT ta thấy để PT (2) có nghiệm trên 1 ; 2
⇔ 0 ≤ 2 m ≤ 4 ⇔ 0 ≤ m ≤ 2



