Các câu hỏi tương tự
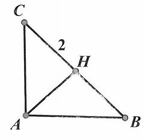
Tam giác ABC vuông cân đỉnh A có cạnh huyền là 2. Quay hình tam giác ABC quanh trục BC thì được khối tròn xoay có thể tích là: A.
2
2
3
π
B.
4
3
π
C.
2
3
π
D.
1
3
π
Đọc tiếp
Tam giác ABC vuông cân đỉnh A có cạnh huyền là 2. Quay hình tam giác ABC quanh trục BC thì được khối tròn xoay có thể tích là:
A. 2 2 3 π
B. 4 3 π
C. 2 3 π
D. 1 3 π
Cho tam giác ABC vuông tại A. Đường thẳng d đi qua A và song song với BC. Cạnh BC quay xung quanh d tạo thành một mặt xung quanh của hình trụ có thể tích là
V
1
. Tam giác ABC quay xung quanh trục d được khối tròn xoay có thể tích là
V
2
. Tính tỉ số
V
1
V
2
.
A.
2...
Đọc tiếp
Cho tam giác ABC vuông tại A. Đường thẳng d đi qua A và song song với BC. Cạnh BC quay xung quanh d tạo thành một mặt xung quanh của hình trụ có thể tích là V 1 . Tam giác ABC quay xung
quanh trục d được khối tròn xoay có thể tích là V 2 . Tính tỉ số V 1 V 2 .
A. 2 3
B. 1 3
C. 3
D. 3 2
Tính thể tích của vật thể giới hạn bởi hai mặt phẳng
x
0
,
x
π
.
Biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với Ox tại điểm có hoành độ
x
0
≤
x
≤
π
là một tam giác vuông cân có cạnh huyền bằng
sin
x
+
2
A.
7...
Đọc tiếp
Tính thể tích của vật thể giới hạn bởi hai mặt phẳng x = 0 , x = π . Biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với Ox tại điểm có hoành độ x 0 ≤ x ≤ π là một tam giác vuông cân có cạnh huyền bằng sin x + 2
A. 7 π 6 + 2
B. 7 π 6 + 1
C. 9 π 8 + 2
D. 9 π 8 + 1
Cho tam giác ABC vuông tại
A
,
AB
6
,
AC
8
.
Quay hình tam giác ABC xung quanh trục BC ta được một khối tròn xoay có thể tích là A.
96
3
π
B.
96
π
C.
384
5
π
D.
1152
5
π
Đọc tiếp
Cho tam giác ABC vuông tại A , AB = 6 , AC = 8 . Quay hình tam giác ABC xung quanh trục BC ta được một khối tròn xoay có thể tích là
A. 96 3 π
B. 96 π
C. 384 5 π
D. 1152 5 π
Cho tam giác ABC vuông tại A,
A
B
6
,
A
C
8
. Quay hình tam giác ABC xung quanh trục BC ta được một khối tròn xoay có thể tích là A.
96
3
π
B.
96
π
C.
384
5
π
D.
1152
5
π
Đọc tiếp
Cho tam giác ABC vuông tại A, A B = 6 , A C = 8 . Quay hình tam giác ABC xung quanh trục BC ta được một khối tròn xoay có thể tích là
A. 96 3 π
B. 96 π
C. 384 5 π
D. 1152 5 π
Cho tứ diện ABCD có
A
D
⊥
A
B
C
,
ABC là tam giác vuông tại B. Biết
B
C
a
,
A
B
a
3
,
A
D
3
a
.
Quay các tam giác ABC và ABD xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối t...
Đọc tiếp
Cho tứ diện ABCD có A D ⊥ A B C , ABC là tam giác vuông tại B. Biết B C = a , A B = a 3 , A D = 3 a . Quay các tam giác ABC và ABD xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng
A. 3 3 π a 3 16
B. 8 3 π a 3 3
C. 5 3 π a 3 16
D. 4 3 π a 3 16
Cho lăng trụ đứng ABC.ABC cạnh bên AA 2, đáy là tam giác vuông cân ABC đỉnh A, canh huyền
B
C
a
2
. Tính thể tích của hình trụ tròn xoay có dáy là hai đường tròn tâm A, bán kính AB và đường tròn tâm A’, bán kính A’B’. A.
V
π
B.
V
2
π
C.
V
3
π
D.
V
4
π
Đọc tiếp
Cho lăng trụ đứng ABC.A'B'C' cạnh bên AA = 2, đáy là tam giác vuông cân ABC đỉnh A, canh huyền B C = a 2 . Tính thể tích của hình trụ tròn xoay có dáy là hai đường tròn tâm A, bán kính AB và đường tròn tâm A’, bán kính A’B’.
A. V = π
B. V = 2 π
C. V = 3 π
D. V = 4 π
Trong không gian, cho tam giác ABC đều cạnh a. Tính thể tích V của khối tròn xoay nhận được khi quay tam giác ABC xung quanh trục BC. A.
V
π
a
3
3
12
B.
V
π
a
3
3
6
C. ...
Đọc tiếp
Trong không gian, cho tam giác ABC đều cạnh a. Tính thể tích V của khối tròn xoay nhận được khi quay tam giác ABC xung quanh trục BC.
A. V = π a 3 3 12
B. V = π a 3 3 6
C. V = π a 3 8
D. V = π a 3 4
Gọi D là diện tích hình phẳng giới hạn bởi các đường
y
sin
2
x
, trục tung, trục hoành và đường thẳng
x
π
. Quay hình phẳng D quay trục Ox ta được khối tròn xoay có thể tích là A.
π
2
. B.
π
2
. C.
π
2
4
. D....
Đọc tiếp
Gọi D là diện tích hình phẳng giới hạn bởi các đường y = sin 2 x , trục tung, trục hoành và đường thẳng x = π . Quay hình phẳng D quay trục Ox ta được khối tròn xoay có thể tích là
A. π 2 .
B. π 2 .
C. π 2 4 .
D. π 2 2 .