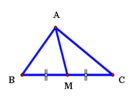
Áp dụng hệ thức đường trung tuyến m a 2 = b 2 + c 2 2 − a 2 4 ta được:
m a 2 = A C 2 + A B 2 2 − B C 2 4 = 12 2 + 9 2 2 − 15 2 4 = 225 4 .
⇒ m a = 15 2 .
Chọn A.
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Tam giác ABC có AB = 9; AC = 12 và BC = 15cm. Tính độ dài đường trung tuyến AM của tam giác đã cho.
A. 7,5
B. 10.
C. 15.
D. 8,5
Cho tam giác đều ABC có cạnh bằng 6cm. Một điểm M nằm trên cạnh BC sao cho BM = 2cm.
a, Tính độ dài của đoạn thẳng AM và tính côsin của góc BAM ;
b, Tính bán kính đường tròn ngoại tiếp tam giác ABM;
c, Tính độ dài đường trung tuyến vẽ từ đỉnh C của tam giác ACM;
d, Tính diện tích tam giác ABM.
Cho tam giác ABC có BC a; CA b; AB c. M là trung điểm của BC, D là chân đường phân giác trong góc A. Tính
A
M
→
2
A. B. C. D.
Đọc tiếp
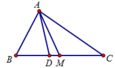
Cho tam giác ABC có BC = a; CA = b; AB = c. M là trung điểm của BC, D là chân đường phân giác trong góc A. Tính A M → 2
A. 
B. 
C. 
D.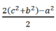 
Cho tam giác ABC có AB =5a, BC=8a, góc ABC=60 , gọi M là trung điểm của BC. Tính theo a độ dài đoạn AM và bán kính đường tròn ngoại tiếp tam giác ABC.
Bài 10:Cho ABC có a 8, b 10, c 13 a. ABC có góc tù hay không ? Tính bán kính đường tròn ngoại tiếp ABC. b. Tính diện tích ABC Bài 11:Cho tam giác ABC có: a 6, b 7, c 5. a) Tính S ,h ,R,r ABC a b) Tính bán kính đường tròn đi qua A, C và trung điểm M của cạnh AB.Bài 12:Cho tam giác ABC có: AB 6, BC 7, AC 8. M trên cạnh AB sao cho MA 2 MB. a) Tính các góc của tam giác ABC. b) Tính S ,h ,R ABC a , r. c) Tính bán kính đường tròn ngoại tiếp ∆MBC.Bài 13:Cho ABC có 0 0 A B b 60 , 45 , 2...
Đọc tiếp
Bài 10:Cho ABC có a = 8, b =10, c =13 a. ABC có góc tù hay không ? Tính bán kính đường tròn ngoại tiếp ABC. b. Tính diện tích ABC
Bài 11:Cho tam giác ABC có: a = 6, b = 7, c = 5. a) Tính S ,h ,R,r ABC a b) Tính bán kính đường tròn đi qua A, C và trung điểm M của cạnh AB.
Bài 12:Cho tam giác ABC có: AB = 6, BC = 7, AC = 8. M trên cạnh AB sao cho MA = 2 MB. a) Tính các góc của tam giác ABC. b) Tính S ,h ,R ABC a , r. c) Tính bán kính đường tròn ngoại tiếp ∆MBC.
Bài 13:Cho ABC có 0 0 A B b = = = 60 , 45 , 2 tính độ dài cạnh a, c, bán kính đường tròn ngoại tiếp và diện tích tam giác ABC
Bài 14:Cho ABC AC = 7, AB = 5 và 3 cos 5 A = . Tính BC, S, a h , R, r.
Bài 15:Cho ABC có 4, 2 m m b c = = và a =3 tính độ dài cạnh AB, AC.
Bài 16:Cho ABC có AB = 3, AC = 4 và diện tích S = 3 3 . Tính cạnh BC
Bài 17:Cho tam giác ABC có ˆ o A 60 = , c h 2 3 = , R = 6. a) Tính độ dài các cạnh của ∆ABC. b) Họi H là trực tâm tam giác ABC. Tính bán kính đường tròn ngoại tiếp ∆AHC.
Bài 18:a. Cho ABC biết 0 0 a B C = = = 40,6; 36 20', 73 . Tính BAC , cạnh b,c. b.Cho ABC biết a m = 42,4 ; b m = 36,6 ; 0 C = 33 10' . Tính AB, và cạnh c.
Bài 19:Tính bán kính đường tròn nội tiếp ABC biết AB = 2, AC = 3, BC = 4.
Bài 20:Cho ABC biết A B C (4 3; 1 , 0;3 , 8 3;3 − ) ( ) ( ) a. Tính các cạnh và các góc của ABC b. Tính chu vi và diện tích ABC
Trong một mặt phẳng tọa độ xOy Cho tam giác ABC biết A(1; - 2) B(-2;3) và C (0;5) A) viết phương trình tham số cạnh AB AC B )viết phương trình tổng quát của đường cao AH và đường trung tuyến AM C)Tính diện tích tam giác ABC
Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Gọi M là một điểm trên cạnh BC và D là chân đường phân giác trong góc A. Tính độ dài vecto MD khi độ dài vecto AM nhỏ nhất
Câu 1: Cho tam giác đều ABC có cạnh là 10a, M là trung điểm của BC. Tính | vec AB + vec AM | ? vec AM . vec BA ? Câu 2: Cho tam giác ABC vuông tại A có AB = 2a căn 3 ; AC = 2a . Tính ? vec AB . vec BC ; | vec AB - vec AC |
Cho tam giác Abc có A(1;2) B(5;0) C(0;1). Viết ptts của a. AB, BC, CA b. Trung tuyến AM c. Đường cao AH d. Đường trung trực của AB