Chọn A.
+ Vì M là trung điểm của BC nên ![]()
Suy ra ![]()
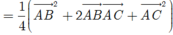
Theo câu trên ta có ![]() nên
nên
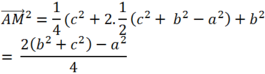
Chọn A.
+ Vì M là trung điểm của BC nên ![]()
Suy ra ![]()
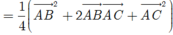
Theo câu trên ta có ![]() nên
nên
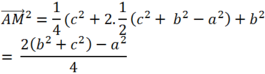
Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Gọi M là một điểm trên cạnh BC và D là chân đường phân giác trong góc A. Tính độ dài vecto MD khi độ dài vecto AM nhỏ nhất
Cho tam giác ABC với AB = c, BC = a, CA = b. Gọi CM là đường phân giác trong của góc C (M∈AB). Biểu thị nào sau đây là đúng?
A. M A → = b a M B →
B. M A → = c a M B →
C. M A → = - b a M B →
D. M A → = - c a M B →
Cho tam giác ABC có D là chân đường phân giác trong, D thuộc BC. Đường thẳng qua D vuông góc với BC cắt phân giác ngoài tại đỉnh A ở I. Vẽ đường tròn (I;ID) cắt AB,AC lần lượt tại E,F. Gọi G là tâm ngoại tiếp tam giác AEF, K là giao điểm của đường đối trung xuất phát từ A của tam giác AEF với (AEF). Chứng minh rằng đường thẳng KG luôn đi qua điểm cố định khi A thay đổi trên cung lớn BC của (ABC).
Cho tam giác ABC với AB= 5 và AC=1. Tính toạ độ điểm D là của chân đường phân giác trong góc A, biết B(7; -2) và C(1;4)
A. 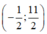
B.(2;3)
C.(0;2)
D.(1;1)
cho tam giác ABC gọi D là chân đường phân giác trong góc B và E là trung điểm BD. đường thẳng qua A song song với BD cắt CE tại F.Cho B (5;1), F(4;3) và điểm A thuộc đường thẳng (d) x+2y-18=0. tính khoảng cách từ gốc tọa độ O đến BC
cho tam giác ABC gọi D là chân đường phân giác trong góc B và E là trung điểm BD. đường thẳng qua A song song với BD cắt CE tại F.Cho B (5;1), F(4;3) và điểm A thuộc đường thẳng (d) x+2y-18=0. tính khoảng cách từ gốc tọa độ O đến BC
Trong mặt phẳng Oxy , cho tam giác ABC có D là chân đường phân giác trong góc B, E là trung điểm BD . Đường thẳng CE cắt phân giác ngoài góc B tại F. Viết phương trình đường thẳng BC biết B(5;1) , F(4;3) và đường thẳng qua A có phương trình là x +2y - 18 =0 .
Trong mpOxy, cho tam giác ABC có A(1; 1), B(3; 3), C(0;-6).
1,Tính cos A.
2,Tìm tọa độ điểm D sao cho tam giác ABD vuông cân tại D.
3,Gọi E là chân đường phân giác trong của góc A.Tìm tọa độ điểm E.
cho tam giác ABC có AB=c BC=a CA=B .. M là trung điểm BC tính \(\overrightarrow{MA}\overrightarrow{BC}\)