Đáp án là A
Tâm các mặt của hình lập phương tạo thành khối bát diện đều
Đáp án là A
Tâm các mặt của hình lập phương tạo thành khối bát diện đều
Cho khối đa diện như hình vẽ bên. Trong đó ABC.A' B' C' là khối lăng trụ tam giác đều có tất cả các cạnh đều bằng 1, S.ABC khối chóp tam giác đều có cạnh bên SA=2/3. Mặt phẳng (SA' B' ) chia khối đa diện đã cho thành hai phần. Gọi V 1 là thể tích phần khối đa diện chứa đỉnh A, V 2 là thể tích phần khối đa diện không chứa đỉnh A. Mệnh đề nào sau đây đúng
A. 72 V 1 = 5 V 2
B. 3 V 1 = V 2
C. 24 V 1 = 5 V 2
D. 4 V 1 = 5 V 2
Cho khối lập phương ABCD.A’B’C’D’. Cắt khối lập phương bởi các mặt phẳng (AB’D’) và (C’BD) ta được ba khối đa diện. Xét các mệnh đề sau:
(I): Ba khối đa diện thu được gồm hai khối chóp tam giác đều và một khối lăng trụ tam giác.
(II): Ba khối đa diện thu được gồm hai khối tứ diện và một khối bát diện đều.
(III): Trong ba khối đa diện thu được có hai khối đa diện bằng nhau.
Số mệnh đề đúng là
A. 3
B. 2
C. 0
D. 1
Cho khối lập phương ABCD.A’B’C’D’. Cắt khối lập phương trên bởi các mặt phẳng (AB’D’) và (C’BD) ta được ba khối đa diện. Xét các mệnh đề sau:
(I): Ba khối đa diện thu được gồm hai khối chóp tam giác đều và một khối lăng trụ tam giác.
(II): Ba khối đa diện thu được gồm hai khối tứ diện và một khối bát diện đều
(III): Trong ba khối đa diện thu được có hai khối đa diện bằng nhau
Số mệnh đề đúng là:
A. 2
B. 1
C. 3
D. 0
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng 1, mặt bên tạo với đáy góc 75 ° . Mặt phẳng (P) chứa đường thẳng AB và tạo với đáy góc 45 ° chia khối chóp S.ABCD thành hai khối đa diện. Thể tích của khối đa diện chứa đỉnh S bằng
A. 16 + 9 3 78
B. 2 + 3 3 1 + 2
C. 2 + 3 6 1 + 2
D. 16 + 9 3 26
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng 1, mặt bên tạo với đáy góc 75o. Mặt phẳng (P) chứa đường thẳng AB và tạo với đáy góc 45o chia khối chóp S.ABCD thành hai khối đa diện. Thể tích của khối đa diện chứa đỉnh S bằng
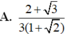
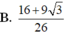
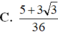
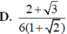
Cho lăng trụ tam giác đều A B C . A ' B ' C ' . Trên A ' B ' kéo dài lấy điểm M sao cho B ' M = 1 2 A ' B . Gọi N, P lần lượt là trung điểm của A ' C ' và B ' B ' . Mặt phàng (MNP) chia khối lăng trụ A B C . A ' B ' C ' thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A ' có thể tích V 1 , khối đa diện chứa đỉnh C ' có thể tích V 2 . Tỉ số V 1 V 2 là:
A. V 1 V 2 = 49 95
B. V 1 V 2 = 49 144
C. V 1 V 2 = 95 144
D. V 1 V 2 = 97 59
Cho lăng trụ tam giác đều ABC.A’B’C’. Trên A’B, kéo dài lấy điểm M sao cho B’M = 1 2 A’B’. Gọi N, P lần lượt là trung điểm của A’C’ và B’B. Mặt phẳng (MNP) chia khối lăng trụ ABC.A’B’C’ thành hai khối đa diện trong đó khối đa diện chứa đỉnh A’ có thể tích V1 và khối đa diện chứa đỉnh C’ có thể tích V2 . Tính V 1 V 2
A. V 1 V 2 = 97 59
B. V 1 V 2 = 49 144
C. V 1 V 2 = 95 144
D. V 1 V 2 = 49 95
Tính thể tích của khối lập phương có các đỉnh là trọng tâm các mặt của khối bát diện đều cạnh a
A. V = 8 a 3 27
B. V = a 3 27
C. V = 16 a 3 2 27
D. V = 2 a 3 2 27
Thể tích V của khối lập phương có các đỉnh là trọng tâm các mặt của một khối bát diện đều cạnh a là
A. V = 8 a 3 27
B. V = a 3 27
C. V = 16 a 3 2 27
D. V = 2 a 3 2 27
Cho khối chóp tứ giác đều S.ABCD. Gọi M là trung điểm SC, mặt phẳng (P) chứa AM và song song với BD chia khối lập phương thành hai khối đa diện, đặt V 1 là thể tích khối đa diện có chứa đỉnh S và V 2 là thể tích khối đa diện có chứa đáy ABCD. Tính V 1 V 2
A. V 1 V 2 = 1 3
B. V 1 V 2 = 1 2
C. V 1 V 2 = 2
D. V 1 V 2 = 3 2