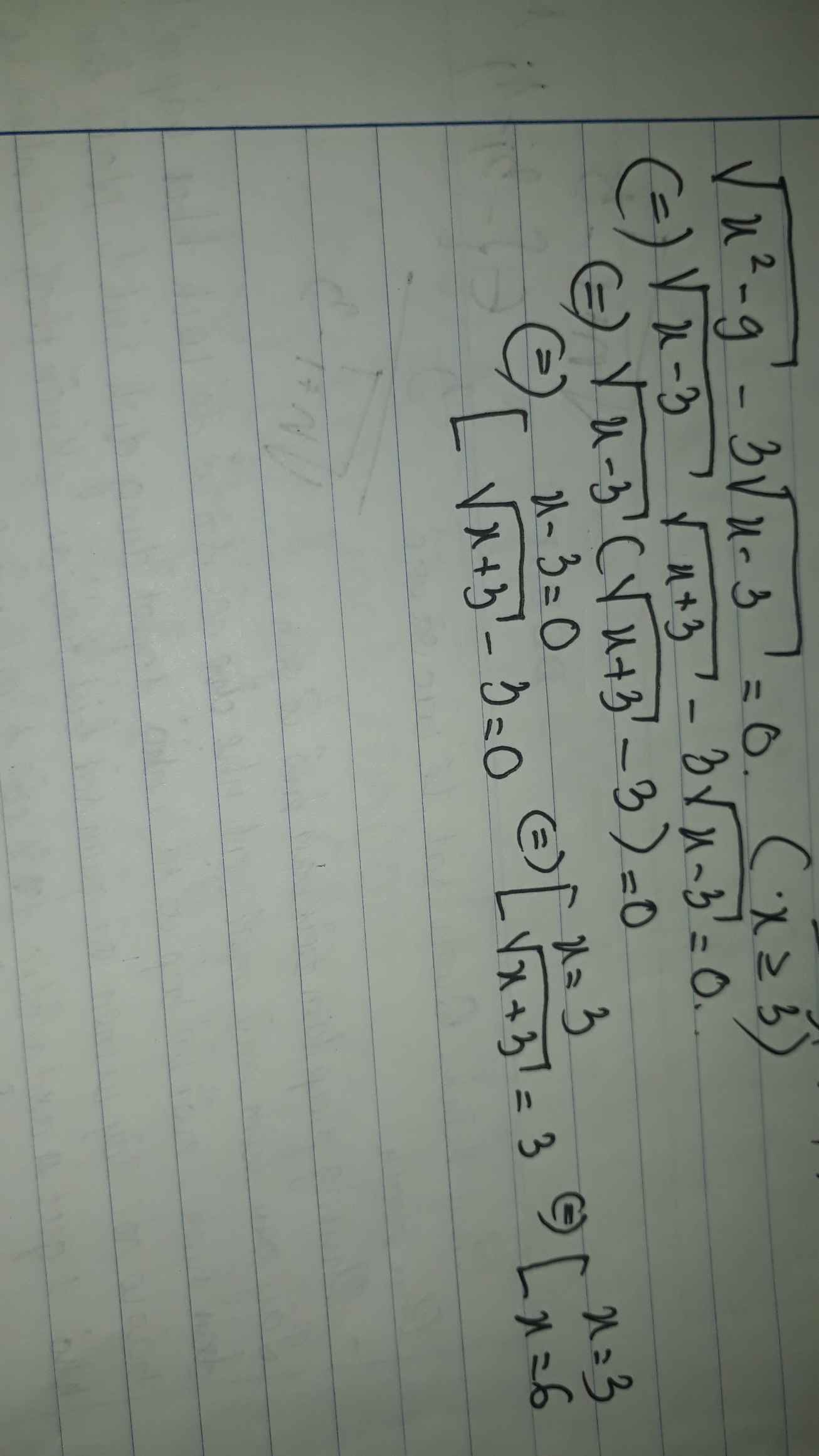Question

\(\sqrt{x^2-9}-3\sqrt{x-3}=0\)

\(\sqrt{\dfrac{4x+3}{x+1}}=3\)

Answer 1

Answer 2

Ta có: \(\sqrt{x^2-9}-3\sqrt{x-3}=0\)

\(\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}-3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+3=9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=6\end{matrix}\right.\)

Answer 3

ĐK: `x>=3`

`\sqrt(x^2-9)-3\sqrt(x-3)=0`

`<=>\sqrt((x-3)(x+3))-3\sqrt(x-3)=0`

`<=>\sqrt(x-3)(\sqrt(x+3)-3)=0`

`<=> [(\sqrt(x-3)=0),(\sqrt(x+3)=3):}`

`<=> [(x-3=0),(x+3=9):}`

`<=> [(x=3),(x=6):}`

Vậy `S={3;6}`.

Answer 4

b) Ta có: \(\sqrt{\dfrac{4x+3}{x+1}}=3\)

\(\Leftrightarrow4x+3=9\left(x+1\right)\)

\(\Leftrightarrow4x-9x=9-3\)

\(\Leftrightarrow-5x=6\)

hay \(x=-\dfrac{6}{5}\)