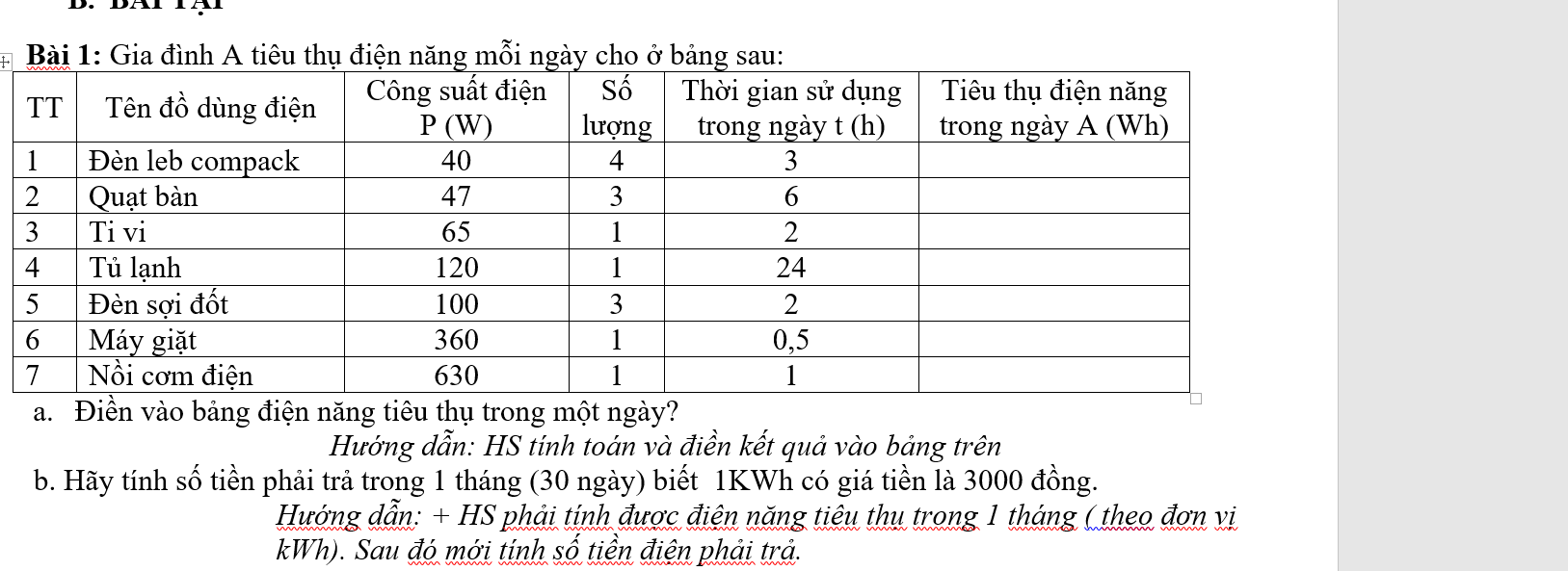
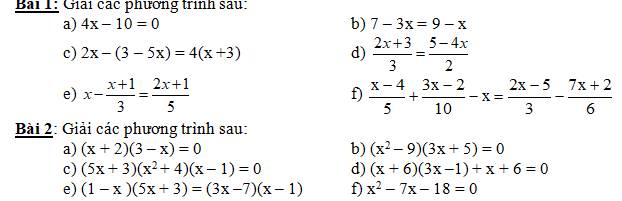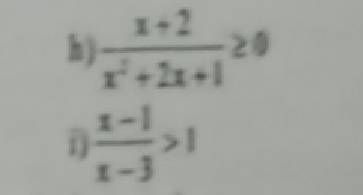Ta có đường thẳng `(d)y=(m+2)x+m`
Có: `a=m+2,b=m`
`a)` Để `(d)`//`(d_1)` thì: `a=-2`
`->m+2=-2`
`->m=-2-2`
`->m=-4`
`b)` Để `(d)\bot(d_1)` thì:
`a*1/3=-1`
`(m+2)*1/3=-1`
`m+2=-1:1/3`
`m+2=-3`
`m=-3-2`
`m=-5`
`c)` Để `(d)` qua điểm `N(1;3)` thì ta thay `x=1,y=3` vào `(d)` ta được:
`3=(m+2)*1+m`
`3=m+2+m`
`2m+2=3`
`2m=3-2`
`2m=1`
`m=1/2`
Vậy: `...`
Cho đường thẳng \(d : y = \left(\right. m + 2 \left.\right) x + m\). Đây là hàm số bậc nhất \(y = a x + b\) với hệ số góc là \(a = m + 2\), tung độ gốc là \(b = m\).
a) Đường thẳng \(d\) song song với đường \(d_{1} : y = - 2 x + 3\)▶ Điều kiện song song: hệ số góc bằng nhau
\(m + 2 = - 2 \Rightarrow m = - 4\)
✅ Đáp án a: \(m = - 4\)
b) Đường thẳng \(d\) vuông góc với đường \(d_{2} : y = \frac{1}{3} x + 1\)▶ Điều kiện vuông góc: tích hệ số góc = -1
\(\left(\right. m + 2 \left.\right) \cdot \frac{1}{3} = - 1 \Rightarrow m + 2 = - 3 \Rightarrow m = - 5\)
✅ Đáp án b: \(m = - 5\)
c) Đường thẳng \(d\) đi qua điểm \(N \left(\right. 1 ; 3 \left.\right)\)▶ Thay \(x = 1\), \(y = 3\) vào phương trình \(y = \left(\right. m + 2 \left.\right) x + m\)
\(3 = \left(\right. m + 2 \left.\right) \cdot 1 + m = m + 2 + m = 2 m + 2 \Rightarrow 2 m = 1 \Rightarrow m = \frac{1}{2}\)
✅ Đáp án c: \(m = \frac{1}{2}\)
📌 Tóm tắt gọn lẹ:
a) Song song: \(m = - 4\)b) Vuông góc: \(m = - 5\)c) Qua điểm \(\left(\right. 1 ; 3 \left.\right)\): \(m = \frac{1}{2}\)