Các câu hỏi tương tự
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như sau:
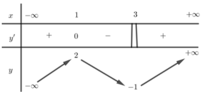
Số nghiệm của phương trình f(x) + 1 = 0 là:
A. 3.
B. 0.
C. 1.
D. 2.
Cho số phức za+bi với a, b là hai số thực khác 0. Một phương trình bậc hai với hệ số thực nhận
z
¯
làm nghiệm với mọi a, b là: A. B. C. D.
Đọc tiếp
Cho số phức z=a+bi với a, b là hai số thực khác 0. Một phương trình bậc hai với hệ số thực nhận z ¯ làm nghiệm với mọi a, b là:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số
y
f
(
x
)
x
3
-
3
x
+
1
.
Số nghiệm của phương trình
f
x
3
-
3
f
(
x
)
+
1...
Đọc tiếp
Cho hàm số y = f ( x ) = x 3 - 3 x + 1 . Số nghiệm của phương trình f x 3 - 3 f ( x ) + 1 = 0 là:
A. 1
B. 6
C. 5
D. 7
Cho phương trình z^2+bc+c0 có hai nghiệm z1 z2 thỏa mãn z2 - z1 4+2i . Gọi A,B là các điểm biểu diễn các nghiệm của phương trình z^2-2bz+4c0 . Tính độ dài đoạn ABA: 8sqrt{5}B: 2sqrt{5}C: 4sqrt{5}D: sqrt{5}
Đọc tiếp
Cho phương trình \(z^2+bc+c=0\) có hai nghiệm z1 z2 thỏa mãn z2 - z1 = 4+2i . Gọi A,B là các điểm biểu diễn các nghiệm của phương trình \(z^2-2bz+4c=0\) . Tính độ dài đoạn AB
A: \(8\sqrt{5}\)
B: \(2\sqrt{5}\)
C: \(4\sqrt{5}\)
D: \(\sqrt{5}\)
Cho bất phương trình
x
4
+
x
2
+
m
3
-
2
x
2
+
1...
Đọc tiếp
Cho bất phương trình x 4 + x 2 + m 3 - 2 x 2 + 1 3 + x 2 x 2 - 1 > 1 - m . Tìm tất cả các giá trị thực của tham số m để bất phương trình trên nghiệm đúng ∀ x > 1 .
![]()
![]()

![]()
Số nghiệm của phương trình l o g 1 4 ( x 2 - x 4 ) = 1 là
A. 1
B. 2
C. 3
D. 4
Cho phương trình az^2+bz+c0 với a,b,c ∈ R , a ≠ 0 có các nghiệm z1,z2 đều không là số thực . Tính P |z1 +z2|2 + |z1 -z2|2 theo a,b,cA: P dfrac{b^2-2ac}{a^2}B: P dfrac{2c}{a}C: Pdfrac{4c}{a}D: P dfrac{2b^2-4ac}{a^2}
Đọc tiếp
Cho phương trình \(az^2+bz+c=0\) với a,b,c ∈ R , a ≠ 0 có các nghiệm z1,z2 đều không là số thực . Tính P |z1 +z2|2 + |z1 -z2|2 theo a,b,c
A: P= \(\dfrac{b^2-2ac}{a^2}\)
B: P= \(\dfrac{2c}{a}\)
C: P=\(\dfrac{4c}{a}\)
D: P= \(\dfrac{2b^2-4ac}{a^2}\)
Gọi
z
1
;
z
2
là các nghiệm phức của phương trình
z
2
+
4
z
+
7
0
. Số phức
z
1
z
2
+
z
1
z
2
bằng A. 2...
Đọc tiếp
Gọi z 1 ; z 2 là các nghiệm phức của phương trình z 2 + 4 z + 7 = 0 . Số phức z 1 z 2 + z 1 z 2 bằng
A. 2
B. 10
C. 2i
D. 10i
Phương trình \(z^2+az+b=0\) với a b là các số thực nhận số phức 1+i là một nghiệm.Tính a - b?
A:-2
B:-4
C:4
D:0





