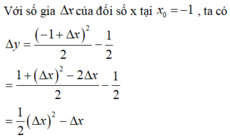Các câu hỏi tương tự
số gia của hàm số y = f(x) = \(\dfrac{^{x^3}}{2}\) ứng với số gia △t của đối số tại x\(_0\) = -1 là :
Số gia của hàm số f(x) = x 3 ứng với x 0 = 2 và ∆ x = 1 bằng bao nhiêu?
A. -19
B. 7
C. 19
D. -7
Số gia của hàm số y = 2 x 2 + 2 tại điểm x0= 0 ứng với số gia ∆x=1 bằng:
A. 2
B. 0
C. -2
D. -8
2. Số gia của hàm số y = 2x^2 -3x +1 theo x và denta x là? 3. Số gia của hàm số y = ✓2x^2 +1 theo x và denta x là?
Số gia của hàm số
f
(
x
)
x
2
ứng với số gia δx của đối số x tại
x
0
-
1
là A.
∆
x
2
-
2
∆
x
-
1
B.
∆
x
2
+
2...
Đọc tiếp
Số gia của hàm số f ( x ) = x 2 ứng với số gia δx của đối số x tại x 0 = - 1 là
A. ∆ x 2 - 2 ∆ x - 1
B. ∆ x 2 + 2 ∆ x + 2
C. ∆ x 2 + 2 ∆ x
D. ∆ x 2 - 2 ∆ x
Cho hàm số
f
(
x
)
x
2
+
2
x
,có ∆x là số gia của đối số tại x1, ∆y là số gia tương ứng của hàm số. Khi đó ∆y bằng: A.
(
∆
x
)
2
+
2
∆
x
B.
(
∆
x
)...
Đọc tiếp
Cho hàm số f ( x ) = x 2 + 2 x ,có ∆x là số gia của đối số tại x=1, ∆y là số gia tương ứng của hàm số. Khi đó ∆y bằng:
A. ( ∆ x ) 2 + 2 ∆ x
B. ( ∆ x ) 2 + 4 ∆ x
C. ( ∆ x ) 2 + 2 ∆ x - 3
D. 3
1) cho hàm số \(f\left(x\right)=\dfrac{1}{3}x^3-2\sqrt{2}x^2+8x-1\) có đạo hàm là f'(x). Tập hợp những giá trị của x để f'(x) = 0
2) cho hàm số \(f\left(x\right)=\dfrac{3-3x+x^2}{x-1}\) giải bất phương trình f'(x) = 0
1. đạo hàm của hàm số f(x) = 2x - 5 tại \(x_0=4\)
2. đạo hàm của hàm số \(y=x^2-3\sqrt{x}+\dfrac{1}{x}\)
3. đạo hàm của hàm số \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt{x}\) tại điểm x = 1
Số gia của hàm số f ( x ) = x 3 ứng với x 0 = 2 và Δx = 1 bằng bao nhiêu?
A.-19
B. 7
C. 19
D. -7