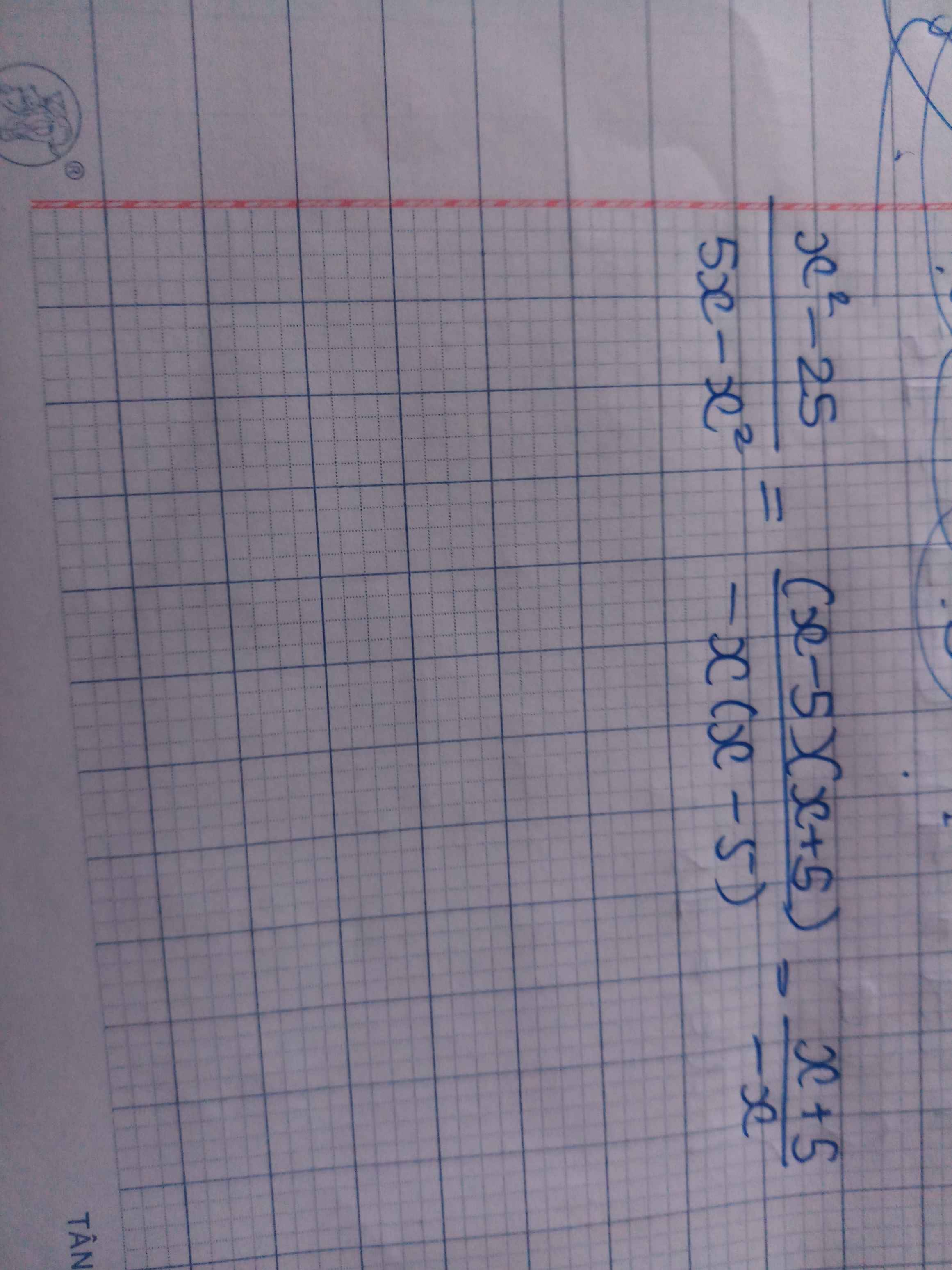Question

Rút gọn 

X²-25

______

5x-x²

Answer 1

Answer 2

\(\dfrac{x^2-25}{5x-x^2}\left(x\ne0;x\ne5\right)\\ =\dfrac{\left(x-5\right)\left(x+5\right)}{x\left(5-x\right)}\\ =-\dfrac{\left(x-5\right)\left(x+5\right)}{x\left(x-5\right)}\\ =\dfrac{-x-5}{x}\)

Answer 3

`(x^2-25)/(5x-x^2)=((x+5)(x-5))/(x(5-x))=(-(x+5)(x-5))/(x(x-5))=(-x-5)/x`

 

Answer 4

\(\dfrac{x^2-25}{5x-x^2}\)

= \(\dfrac{\left(x+5\right)\left(x-5\right)}{x\left(5-x\right)}\)

= \(-\left[\dfrac{\left(x+5\right)\left(x-5\right)}{x\left(5-x\right)}\right]\)

= \(\dfrac{\left(x+5\right)\left(x-5\right)}{x\left(-5+x\right)}\)

= \(\dfrac{\left(x+5\right)\left(x-5\right)}{x\left(x-5\right)}\)

= \(\dfrac{x+5}{x}\)

Answer 5

\(\dfrac{x^2-25}{5x-x^2}=\dfrac{\left(x+5\right)\left(x-5\right)}{-x\left(x-5\right)}=\dfrac{x+5}{-x}\)

Answer 6

\(\dfrac{x^2-25}{5x-x^2}=\dfrac{\left(x-5\right)\left(x+5\right)}{-x\left(x-5\right)}=\dfrac{-x-5}{x}\)