Chọn đáp án B.
Áp dụng quy tắc nhân các căn bậc hai ta có:
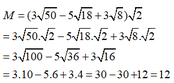
Chọn đáp án B.
Áp dụng quy tắc nhân các căn bậc hai ta có:
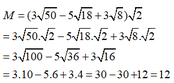
tính và rút gọn các biểu thức
a) 3 √8 - 4 √18 + 2 √50
b) 5 √12 +2 √75 - 5 √48
Câu 1
Rút gọn biểu thức A = √24 + 2√54 - 2√96
Câu 2
Rút gọn biểu thức A = 3√48 + √75 - 2√108
Câu 3
Rút gọn biểu thức A = √18 - 2√50 + 3√8
Câu 4
Tính giá trị biểu thức A = √18 + 2√8 - \(\dfrac{1}{5}\)√50
Câu 5
Rút gọn biểu thức M = √20 - √45 + √5
Câu 6
Tính giá trị biểu thức A = √5.(√5-3) + √45
Rút gọn các biểu thức sau a)√27-✓12+✓48-5✓3 b)5✓18-✓5+✓20+✓1 2 C)✓25:✓16=✓36:✓9 D)✓12+✓27-5✓3 E)2✓3-✓75+2✓12
Rút gọn các biểu thức sau :
a) A= \(\sqrt{18}\) . \(\sqrt{2}\) - \(\sqrt{48}\) : \(\sqrt{3}\)
b)B= \(\dfrac{8}{\sqrt{5}-1}\) + \(\dfrac{8}{\sqrt{5}+1}\)
rút gọn các câu sau
a,\(2\sqrt{18}-4\sqrt{50}+3\sqrt{32}\)
b,\(\sqrt{\left(\sqrt{8}-4\right)^2}+\sqrt{8}\)
c,\(\sqrt{14-6\sqrt{5}}+\sqrt{6+2\sqrt{5}}\)
rút gọn biểu thức
A=2015+\(\sqrt{36}\)-\(\sqrt{25}\)
B=5\(\sqrt{8}\)+\(\sqrt{50}\)-2\(\sqrt{18}\)
C=\(\sqrt{27}\)-2\(\sqrt{12}\)-\(\sqrt{75}\)
D=\(\sqrt{12}\)+\(\sqrt{27}\)-\(\sqrt{48}\)
(1) rút gọn biểu thức:
a) A= \(3\sqrt{2}+5\sqrt{8}-2\sqrt{50}\)
b) B= \(\sqrt{7-4\sqrt{3}}+\sqrt{12+6\sqrt{3}}\)
c) C= \(\dfrac{1}{3+\sqrt{5}}+\dfrac{1}{3-\sqrt{5}}\)
d) D= \(\sqrt[3]{27}-\sqrt[3]{-8}-\sqrt[3]{125}\)
giúp mk vs ạ mai mk hc rồi
Rút gọn biểu thức
a) √2 + √8 + √50;
b) 4√3 + √27 - √45 + √5.
Rút gọn các biểu thức sau:
a) \(0,2\sqrt{\left(-10\right)^2.3}+2\sqrt{\left(\sqrt{3}-\sqrt{5}\right)^2}\) b) \(\left(15\sqrt{50}+5\sqrt{200}-3\sqrt{450}\right):\sqrt{10}\)
c) \(\left(\frac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\frac{\sqrt{216}}{3}\right):\sqrt{6}\) d) \(\frac{\sqrt{5+2\sqrt{6}}+\sqrt{8-2\sqrt{15}}}{\sqrt{7+2\sqrt{10}}}\)
Rút gọn các biểu thức
\(B=\frac{9\sqrt{5}+3\sqrt{27}}{\sqrt{5}+\sqrt{3}} \)
\(C=\frac{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+4}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)
\(D=\frac{3\sqrt{8}-2\sqrt{12}+20}{3\sqrt{18}-2\sqrt{27}+\sqrt{45}}\)