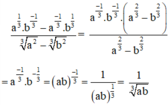Các câu hỏi tương tự
Rút gọn biểu thức
P
a
2
b
(
a
b
-
2
)
-
3
(
a
-
2
b
-...
Đọc tiếp
Rút gọn biểu thức P = a 2 b ( a b - 2 ) - 3 ( a - 2 b - 1 ) - 2 viết kết quả sao cho các lũy thừa đều dương
A. P = a 3 b 9
B. P = b a 5
C. P = b a 3
D. P = a b 5
RÚT GỌN BIỂU THỨC:
17) \(A = \left(\dfrac{\sqrt{x} - 1}{3\sqrt{x} - 1} - \dfrac{1}{3\sqrt{x} + 1} + \dfrac{8\sqrt{x}}{9x - 1}\right) : \left(1 - \dfrac{3\sqrt{x} - 2}{3\sqrt{x} + 1}\right)\)
Rút gọn biểu thức
P
a
3
b
3
-
1
3
+
1
.
a
-
1...
Đọc tiếp
Rút gọn biểu thức
P = a 3 b 3 - 1 3 + 1 . a - 1 - 3 b - 2 a , b > 0
![]()
![]()
![]()
![]()
Tìm khẳng định sai trong các khẳng định sau:A.
2
-
2
1 B.
0
,
013
-
1
75A.
π
4
5
-...
Đọc tiếp
Tìm khẳng định sai trong các khẳng định sau:
A. 2 - 2 < 1 B. 0 , 013 - 1 > 75
A. π 4 5 - 2 > 1 B. 1 3 8 - 3 < 3
Cho
I
∫
0
π
2
2
x
-
1
-
sin
x
d
x
. Biết
I
π
2
a...
Đọc tiếp
Cho I = ∫ 0 π 2 2 x - 1 - sin x d x . Biết I = π 2 a - π b - 1
Cho các mệnh đề sau:
Các phát biểu đúng
(1) a = 2b (2) a + b = 5 (3) a +3b = 10 (4) 2a + b = 10
A. (1),(2),(3)
B. (2),(3),(4)
C. (1),(2),(4)
D. (1),(3),(4)
cho hai số a,b là hai số thực đều lớn hơn 1. giá trị nhỏ nhất của biểu thức s=
\(\dfrac{1}{log_{b\sqrt[3]{a}}}\)+\(\dfrac{1}{log\sqrt[3]{ab^2}}\)
Rút gọn biểu thức
1
4
y
-
1
5
-
1
+
3
-
1
. A. 8 B.
4
y
-
1
8
C.
1...
Đọc tiếp
Rút gọn biểu thức 1 4 y - 1 5 - 1 + 3 - 1 .
A. 8
B. 4 y - 1 8
C. 15 2
D. 15 8
Cho x,y,z,a,b,c là các số thực thay đổi thỏa mãn
(
x
+
3
)
2
+
(
y
-
2
)
2
+
(
z
+
1
)...
Đọc tiếp
Cho x,y,z,a,b,c là các số thực thay đổi thỏa mãn ( x + 3 ) 2 + ( y - 2 ) 2 + ( z + 1 ) 2 = 2 và a+b+c=1. Giá trị nhỏ nhất của biểu thức P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 là
A. 3 - 2
B. 3 + 2
C. 5 - 2 6
D. 5 + 2 6
rút gọn: A= \(\frac{\frac{3}{2}+\frac{2}{5}+\frac{1}{10}}{\frac{3}{2}+\frac{2}{3}+\frac{1}{12}}\)
Tính giá trị bằng số của biểu thức 9 log 3 2
A. 2 B. 4
C. 1/3 D. 1/2