a: \(\dfrac{10+2\sqrt{10}}{\sqrt{5}+\sqrt{2}}\)
\(=\dfrac{\sqrt{100}+\sqrt{40}}{\sqrt{5}+\sqrt{2}}\)
\(=\dfrac{\sqrt{20}\left(\sqrt{5}+\sqrt{2}\right)}{\sqrt{5}+\sqrt{2}}=\sqrt{20}=2\sqrt{5}\)
c: \(\dfrac{\sqrt{2}}{\sqrt{5}-\sqrt{3}}\)
\(=\dfrac{\sqrt{2}\left(\sqrt{5}+\sqrt{3}\right)}{\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)}\)
\(=\dfrac{\sqrt{10}+\sqrt{6}}{5-3}=\dfrac{\sqrt{10}+\sqrt{6}}{2}\)
e: \(\left(\dfrac{15}{\sqrt{6}+1}+\dfrac{4}{\sqrt{6}-2}-\dfrac{12}{3-\sqrt{6}}\right)\left(\sqrt{6}+11\right)\)
\(=\left(\dfrac{15\left(\sqrt{6}-1\right)}{6-1}+\dfrac{4\left(\sqrt{6}+2\right)}{6-4}-\dfrac{12\left(3+\sqrt{6}\right)}{9-6}\right)\cdot\left(\sqrt{6}+11\right)\)
\(=\left[3\left(\sqrt{6}-1\right)+2\left(\sqrt{6}+2\right)-4\left(3+\sqrt{6}\right)\right]\left(\sqrt{6}+11\right)\)
\(=\left(3\sqrt{6}-3+2\sqrt{6}+4-12-4\sqrt{6}\right)\left(\sqrt{6}+11\right)\)
\(=\left(\sqrt{6}-11\right)\left(\sqrt{6}+11\right)\)
=6-121
=-115
g: \(\dfrac{1}{\sqrt{5}+1}+\dfrac{1}{\sqrt{5}-2}-\dfrac{1}{3-\sqrt{5}}-\sqrt{5}\)
\(=\dfrac{\sqrt{5}-1}{4}+\dfrac{\sqrt{5}+2}{1}-\dfrac{1\left(3+\sqrt{5}\right)}{4}-\sqrt{5}\)
\(=\dfrac{1}{4}\sqrt{5}-\dfrac{1}{4}+\sqrt{5}+2-\dfrac{3}{4}-\dfrac{\sqrt{5}}{4}-\sqrt{5}\)
\(=-1+2=1\)

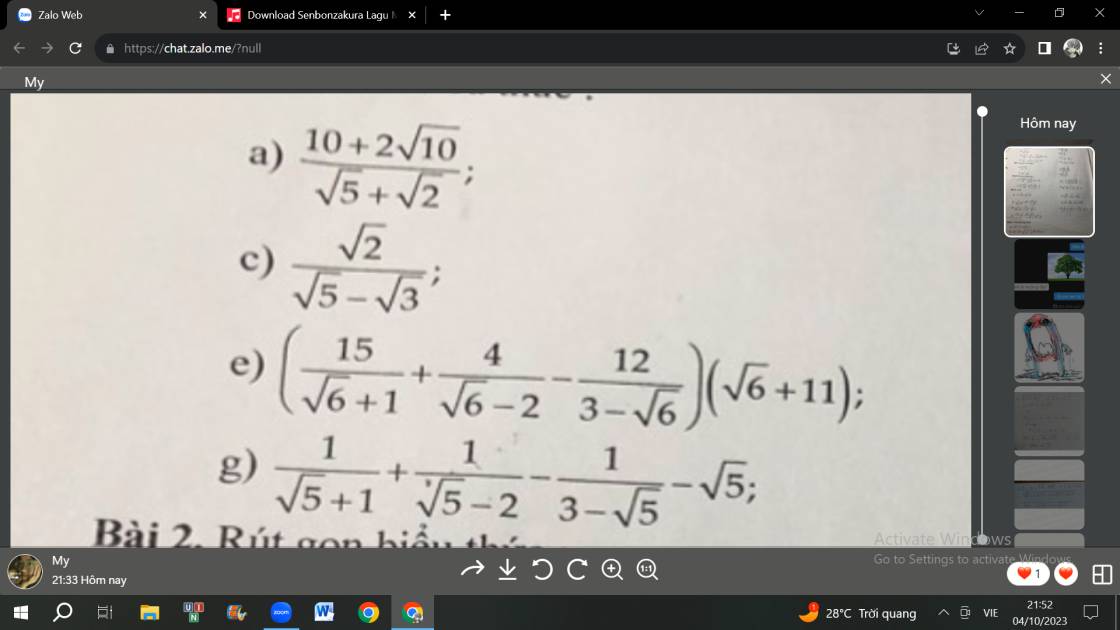




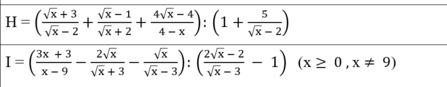
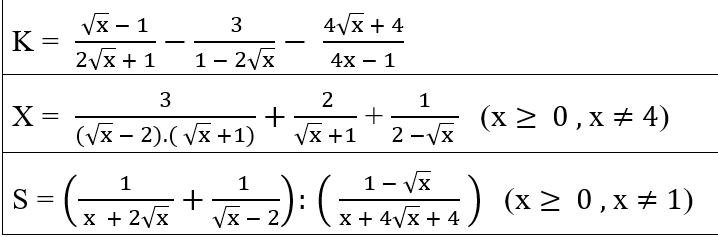
 Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.![[柠檬]๛Čɦαŋɦ ČŠツ](https://hoc24.vn/images/avt/avt6342624_256by256.jpg)




