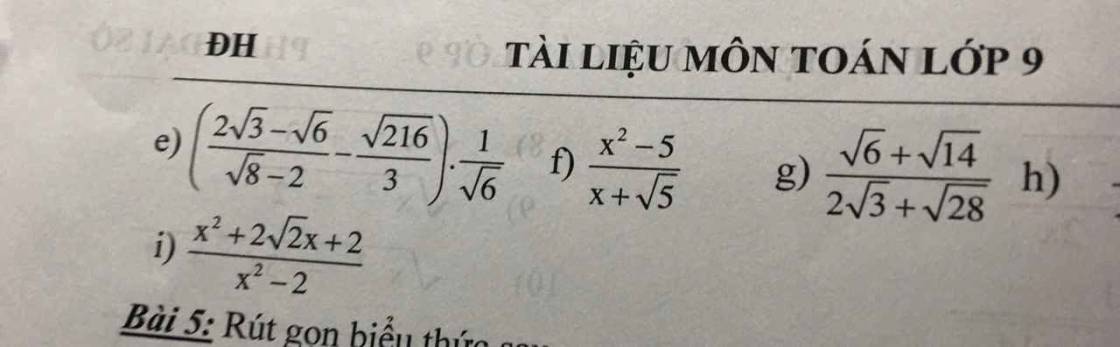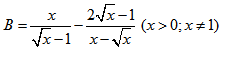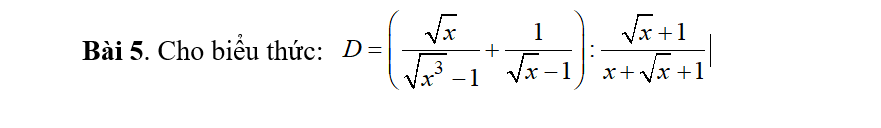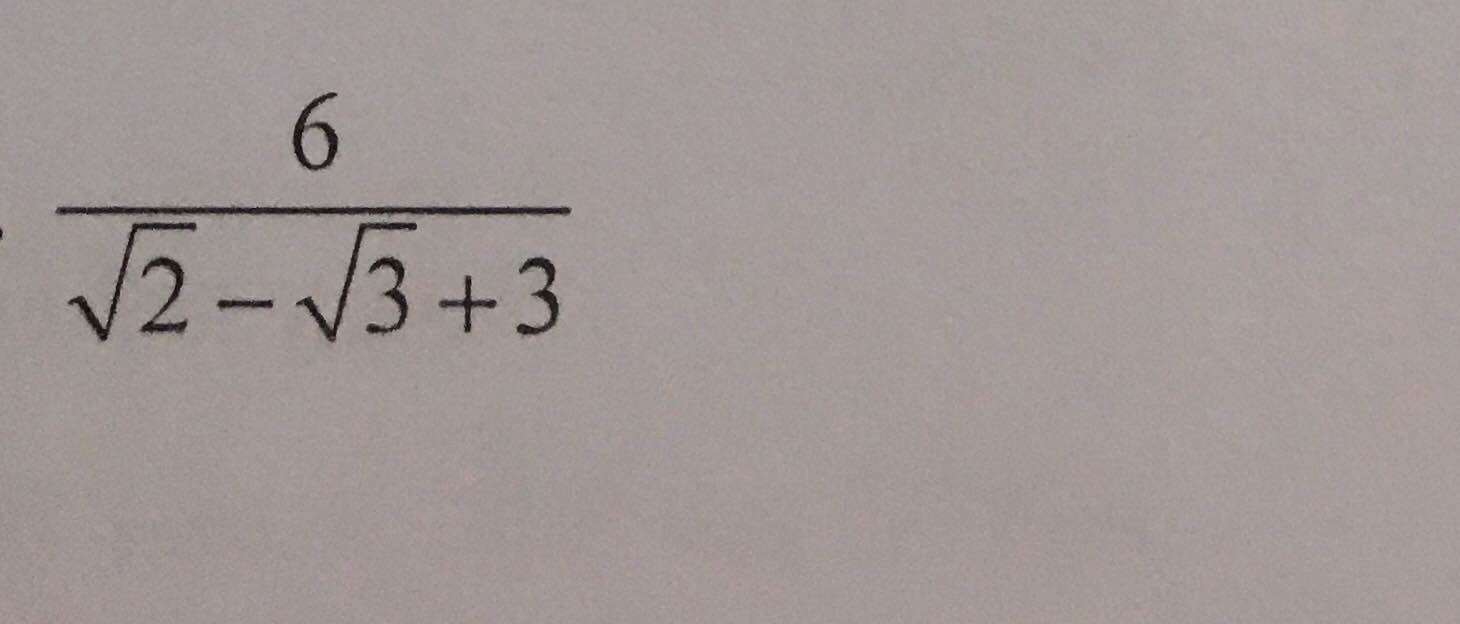\(e,\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right).\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\sqrt{2}-2}-\dfrac{6\sqrt{6}}{3}\right).\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}-2\sqrt{6}\right).\dfrac{1}{\sqrt{6}}\)
\(=\dfrac{\sqrt{6}-4\sqrt{6}}{2}.\dfrac{1}{\sqrt{6}}\)
\(=\dfrac{-3\sqrt{6}}{2}.\dfrac{1}{\sqrt{6}}\)
\(=-\dfrac{3}{2}\)
\(f,\dfrac{x^2-5}{x+\sqrt{5}}=\dfrac{\left(x-\sqrt{5}\right)\left(x+\sqrt{5}\right)}{x+\sqrt{5}}=x-\sqrt{5}\)
\(g,\dfrac{\sqrt{6}+\sqrt{14}}{2\sqrt{3}+\sqrt{28}}=\dfrac{\sqrt{2}.\sqrt{3}+\sqrt{2}.\sqrt{7}}{2\sqrt{3}+2\sqrt{7}}=\dfrac{\sqrt{2}\left(\sqrt{3}+\sqrt{7}\right)}{2\left(\sqrt{3}+\sqrt{7}\right)}=\dfrac{\sqrt{2}}{2}\)
\(i,\dfrac{x^2+2\sqrt{2}x+2}{x^2-2}=\dfrac{\left(x+\sqrt{2}\right)^2}{\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)}=\dfrac{x+\sqrt{2}}{x-\sqrt{2}}\)