
⇒ A ^ + B S M ^
= 1 2 . s đ N C ⏜ - s đ B M ⏜ + 1 2 s đ N C ⏜ + s đ M B ⏜ = s đ N C ⏜ 1
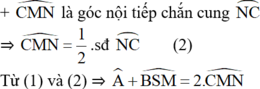
(đpcm)


⇒ A ^ + B S M ^
= 1 2 . s đ N C ⏜ - s đ B M ⏜ + 1 2 s đ N C ⏜ + s đ M B ⏜ = s đ N C ⏜ 1
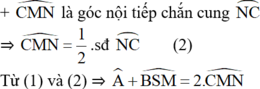
(đpcm)
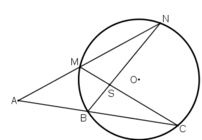
Qua điểm A nằm bên ngoài đường tròn (O) vẽ hai cát tuyến ABC và AMN sao cho hai đường thẳng BN và CM cắt nhau tại một điểm S nằm bên tròn đường tròn.
Chứng minh A ^ + B S M ⏞ = 2 ⋅ C M N ⏞
cho điểm A bên ngoài đường tròn (O) vẽ 2 cát tuyến ABC và AMN sao cho 2 đường thẳng BN và CM cắt nhau tại điểm S nằm bên trong đường tròn.
Chứng minh :
\(\widehat{A}\)+\(\widehat{BSM}\)= \(2.\widehat{CMN}\)
Từ một điểm A nằm bên ngoài đường tròn (O) kẻ hai tiếp tuyến AB, AC với đường tròn (O) (B, C là tiếp điểm). Một đường thẳng (d) đi qua A cắt đường tròn (O) tại hai điểm D và E (d không đi qua tâm O, D nằm giữa A và E), gọi I là trung điểm của DE. BC cắt AE tại S. Qua C kẻ đường thẳng song song với AB, đường thẳng này cắt các đường thẳng BE, BD lần lượt tại M và N. CM: C là trung điểm MN.
Cho điểm A nằm ngoài đường tròn (O). Qua A kẻ hai tiếp tuyến AB và AC với (O) (B, C là tiếp điểm). Kẻ cát tuyến AMN với (O) (M nằm giữa A và N)
a, Chứng minh A B 2 = A M . A N
b, Gọi H = AO ∈ BC. Chứng minh AH.AO = AM.AN
c, Đoạn thẳng AO cắt đường tròn (O) tại I. Chứng minh I là tâm đường tròn nội tiếp tam giác ABC
Từ một điểm A nằm bên ngoài đường tròn (O) kẻ hai tiếp tuyến AB, AC với đường tròn (O) (B, C là tiếp điểm). Một đường thẳng (d) đi qua A cắt đường tròn (O) tại hai điểm D và E (d không đi qua tâm O, D nằm giữa A và E), gọi I là trung điểm của DE. BC cắt AE tại S. Qua C kẻ đường thẳng song song với AB, đường thẳng này cắt các đường thẳng BE, BD lần lượt tại M và N. CM: C là trung điểm MN.
Giúp mình bài này với.
Cho đường tròn (O) và điểm A nằm bên ngoài đường tròn (O). Qua điểm A dựng hai tiếp tuyến AM,AN đến đường tròn (O) với M,N là các tiếp điểm. Một đường thẳng d đi qua A cắt đường tròn (O) tại hai điểm B và C (AB<AC, đường thẳng d không đi qua tâm O)
a) Chứng minh tứ giác AMON là tứ giác nội tiếp
b) Chứng minh AN\(^2\)=AB.AC
c) Hai tiếp tuyến của đường trong (O) tại B và C cắt nhau tại K. Chứng minh rằng điểm K luôn thuộc một đường thẳng cố định khi đường thẳng d thay đổi và đường thẳng d thỏa mãn điều kiện đề bài
Cho đường tròn (O) và điểm A nằm bên ngoài đường tròn (O). Qua điểm A dựng hai tiếp tuyến AM,AN đến đường tròn (O) với M,N là các tiếp điểm. Một đường thẳng d đi qua A cắt đường tròn (O) tại hai điểm B và C (AB<AC, đường thẳng d không đi qua tâm O)
a) Chứng minh tứ giác AMON là tứ giác nội tiếp
b) Chứng minh AN=AB.AC
c) Hai tiếp tuyến của đường trong (O) tại B và C cắt nhau tại K. Chứng minh rằng điểm K luôn thuộc một đường thẳng cố định khi đường thẳng d thay đổi và đường thẳng d thỏa mãn điều kiện đề bài
Giúp mình với đang cần gấp lắm!!
cho đường tròn (O;R) A là điểm nằm bên ngoài đường tròn. Từ A kẻ 2 tiếp tuyến AB ,AC với đường tròn (O;R) (B và C là hai tiếp điểm)
a. Chứng minh tứ giác ABOC nội tiếp đường tròn
b. Kẻ cát tuyến AMN (M nằm giữa A và N). Chứng minh AB^2 = AM.AN
c. Gọi K là giao điểm của tia CM và AB. Chứng minh góc ABC = góc KMB
Cho đường tròn (O;R) và một điểm A nằm ngoài đường tròn. Kẻ một đường thẳng qua A và không đi qua tâm O, cắt đường tròn tại 2 điểm phân biệt M, N (M nằm giữa A và N). Từ A vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là hai tiếp điểm). Đường thẳng BC cắt AO tại H. Gọi I là trung điểm của MN.
a) Chứng minh tứ giác ACOI là tứ giác nội tiếp.
b) Chứng minh OI.OE = OH.OA = AC2.
c) Tính theo R độ dài của OA biết diện tích của tứ giác ABOC bằng 3R2.
b bic làm bài này hok z
giúp mik vs ạ