Các câu hỏi tương tự
Có bao nhiêu giá trị nguyên của tham số m để phương trình
6
+
x
-
2
-
x
-
3
+
x
-
6
-
x
-
5
-
m
0
có nghiệm thực A. 0 B. 2 C. 3 D. 1
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình 6 + x - 2 - x - 3 + x - 6 - x - 5 - m = 0 có nghiệm thực
A. 0
B. 2
C. 3
D. 1
Gọi a là số thực lớn nhất để bất phương trình
x
2
-
x
+
2
+
a
ln
x
2
-
x
+
1
≥
0
nghiệm đúng với mọi
x
∈
ℝ
. Mệnh đề nào sau đây đúng? A.
a
∈
(
2
;
3...
Đọc tiếp
Gọi a là số thực lớn nhất để bất phương trình x 2 - x + 2 + a ln x 2 - x + 1 ≥ 0 nghiệm đúng với mọi x ∈ ℝ . Mệnh đề nào sau đây đúng?
A. a ∈ ( 2 ; 3 ]
B. a ∈ 8 ; + ∞
C. a ∈ ( 6 ; 7 ]
D. a ∈ ( - 6 ; - 5 ]
Gọi a là số thực lớn nhất để bất phương trình
x
2
−
x
−
2
+
a
ln
x
2
−
x
+
1
≥
0
nghiệm đúng với mọi
x
∈
ℝ
.
Mệnh đề nào sau đây đúng? A.
a
∈
6...
Đọc tiếp
Gọi a là số thực lớn nhất để bất phương trình x 2 − x − 2 + a ln x 2 − x + 1 ≥ 0 nghiệm đúng với mọi x ∈ ℝ . Mệnh đề nào sau đây đúng?
A. a ∈ 6 ; 7 .
B. a ∈ 2 ; 3 .
C. a ∈ − 6 ; − 5 .
D. a ∈ 8 ; + ∞
Gọi a là số thực lớn nhất để bất phương trình
x
2
−
x
+
2
+
a
ln
x
2
−
x
+
1
≥
0
nghiệm đúng với mọi
x
∈
ℝ
.
Mệnh đề nào sau đây đúng? A.
a
∈
6...
Đọc tiếp
Gọi a là số thực lớn nhất để bất phương trình x 2 − x + 2 + a ln x 2 − x + 1 ≥ 0 nghiệm đúng với mọi x ∈ ℝ . Mệnh đề nào sau đây đúng?
A. a ∈ 6 ; 7
B. a ∈ 2 ; 3
C. a ∈ − 6 ; − 5
D. a ∈ 8 ; + ∞
Gọi a là số thực lớn nhất để bất phương trình
x
2
-
x
+
2
+
a
ln
(
x
2
-
x
+
1
)
≥
0
nghiệm đúng với mọi
x
∈
R
. Mệnh đề nào sau đây đúng? A.
a
∈
(
8
;
+
∞
)
B.
a...
Đọc tiếp
Gọi a là số thực lớn nhất để bất phương trình x 2 - x + 2 + a ln ( x 2 - x + 1 ) ≥ 0 nghiệm đúng với mọi x ∈ R . Mệnh đề nào sau đây đúng?
A. a ∈ ( 8 ; + ∞ )
B. a ∈ ( - 6 ; - 5 )
C. a ∈ ( 6 ; 7 )
D. a ∈ ( 2 ; 3 )
Cho các mệnh đề sau đây:(1) Hàm số
f
(
x
)
log
2
2
x
-
log
2
x
4
+
4
có tập xác định
D
[
0
;
+
∞
)
(2) Hàm số
y
log
a
x
có tiệm cận ngang(3) Hàm số
y
log
a
x
;
...
Đọc tiếp
Cho các mệnh đề sau đây:
(1) Hàm số f ( x ) = log 2 2 x - log 2 x 4 + 4 có tập xác định D = [ 0 ; + ∞ )
(2) Hàm số y = log a x có tiệm cận ngang
(3) Hàm số y = log a x ; 0 < a < 1 và Hàm số y = log a x , a > 1 đều đơn điệu trên tập xác định của nó
(4) Bất phương trình: log 1 2 5 - 2 x 2 - 1 ≤ 0 có 1 nghiệm nguyên thỏa mãn.
(5) Đạo hàm của hàm số y = ln 1 - cos x là sin x 1 - cos x 2
Hỏi có bao nhiêu mệnh đề đúng:
A. 0
B. 2
C. 3
D.1
Bài 1: giải các phương trình sau:
a) 2(x+5) - x2 - 5x = 0 b) 2x2 + 3x - 5 = 0 c) ( x - 1)2 + 4(x+2) - (x2 - 3 ) = 0
Cho hàm số y f (x) có bảng biến thiên như sauSố nghiệm thực của phương trình 2 f (x) + 3 0 là A. 4 B. 3 C. 2 D. 1
Đọc tiếp
Cho hàm số y = f (x) có bảng biến thiên như sau
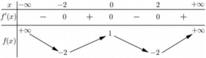
Số nghiệm thực của phương trình 2 f (x) + 3 = 0 là
A. 4
B. 3
C. 2
D. 1
a) Cho tam giác ABC có C(-1;-2) đường trung tuyến kẻ từ A và đường cao kẻ từ B lần lượt có phương trình 5x+y-9=0 và x+3y-5=0. Tìm tọa độ A, B
b) Cho đường thẳng a: x-2y-3=0 và b: x+y+1=0. Tìm tọa độ điểm M trên a sao cho khoảng cách từ M đến b là 1/ căn 2
Giải phương trình
a) \(\frac{4}{20-6x-2x^2}\)+ \(\frac{x^2+4x}{x^2+5x}-\frac{x+3}{2-x}+3=0\)
b)\(\frac{x+5}{x^2-5x}-\frac{x-5}{2x^2-10x}+10=\frac{x+25}{2x^2-50}\)
c) \(\frac{7}{8x}+\frac{5-x}{4x^2-8x}=\frac{x-1}{2x.\left(x-2\right)}+\frac{1}{8x-16}\)






