Cho hàm số f(x) xác định trên K.
Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K
⇔ F’(x) = f(x) ∀ x ∈ K.
Cho hàm số f(x) xác định trên K.
Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K
⇔ F’(x) = f(x) ∀ x ∈ K.
Phát biểu định nghĩa tích phân của hàm số f(x) trên một đoạn.
Cho các phát biểu sau:
I. Đồ thị hàm số có y = x4 – x + 2 có trục đối xứng là Oy.
II. Hàm số f(x) liên tục và có đạo hàm trên khoảng (a;b) đạt cực trị tại điểm x0 thuộc khoảng (a;b) thì tiếp tuyến tại điểm M(x0,f(x0)) song song với trục hoành.
III. Nếu f(x) nghịch biến trên khoảng (a;b) thì hàm số không có cực trị trên khoảng (a;b).
IV. Hàm số f(x) xác định và liên tục trên khoảng (a;b) và đạt cực tiểu tại điểm x0 thuộc khoảng (a;b) thì f(x) nghịch biến trên khoảng (a;x0) và đồng biến trên khoảng (x0;b).
Các phát biểu đúng là:
A. II,III,IV
B. I,II,III
C. III,IV
D. I,III,IV
Cho F(x) là nguyên hàm của hàm số f(x) trên [a; b]. Phát biểu nào sau đây sai?
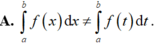
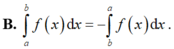
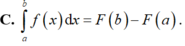
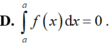
Cho hàm số f liên tục trên đoạn [a;b] có một nguyên hàm là hàm F trên đoạn [a;b]. Trong các phát biểu sau, phát biểu nào sai?
A. ∫ a b f x d x = F b - F a
B. F ' x = f x v ớ i m ọ i x ∈ a ; b
C. ∫ a b f x d x = f b - f a
D. Hàm số G cho bởi G ( x ) = F ( x ) + 5 cũng thỏa mãn ∫ a b f x d x = G b - G a
Biết rằng x e x là một nguyên hàm của hàm số f(-x) trên khoảng - ∞ , + ∞ . Gọi F(x) là một nguyên hàm của f ' x e x thỏa mãn F(0) =1, giá trị của F(-1) bằng:
A. 7 2
B. 5 - e 2
C. 7 - e 2
D. 5 2
Cho hàm số f(x) liên tục trên khoảng (-2; 3). Gọi F(x) là một nguyên hàm của f(x) trên khoảng (-2; 3). Tính 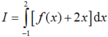 , biết F(-1) = 1, F(2) = 4.
, biết F(-1) = 1, F(2) = 4.
A. I = 6.
B. I = 10.
C. I = 3.
D. I = 9.
Cho hàm số F(x) là một nguyên hàm của hàm số f ( x ) = 2 cos x - 1 sin 2 x trên khoảng 0 ; π . Biết rằng giá trị lớn nhất của F(x) trên khoảng 0 ; π là 3 . Chọn mệnh đề đúng trong các mệnh đề sau?

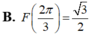
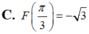
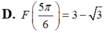
Phát biểu các điều kiện cần và đủ để hàm số f(x) đơn điệu trên một khoảng.
Cho hàm số F(x) là một nguyên hàm của hàm số f(x) xác định trên K. Mệnh đề nào dưới đây sai?
![]()
![]()
![]()
![]()