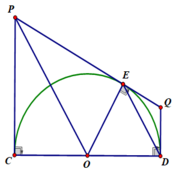
Xét tứ giác CPEO có:
∠(PCO) = ∠(PEO) = 90 0 (gt)
⇒ ∠(PCO) + ∠(PEO) = 180 0
⇒ Tứ giác CPEO là tứ giác nội tiếp
Xét tứ giác OEQD có:
∠(OEQ) = ∠(ODQ) = 90 0 (gt)
⇒ ∠(OEQ) + ∠(ODQ) = 180 0
⇒ Tứ giác OEQD là tứ giác nội tiếp
Cho nửa đường tròn tâm O bán kính CD. Từ C,D kẻ các tiếp tuyến Cx,Dy với nửa đường tròn tâm O.
Trên nửa đường tròn lấy điểm E, điểm M bất kì nằm trên CD(M khác C,D,O).Qua E kẻ đường thẳng vuông góc với EM và cắt Cx,Dy tại A,B.C/m góc AMB =90o
Cho nữa đường tròn(O;R) đường kính CD. Trên nửa mặt phẳng chứa nửa đường tròn vẽ các tia Cx, Dy cùng vuông góc với CD. Qua điểm E thuộc nửa đường tròn(E khác C và D) kẻ tiếp tuyến với nửa đường tròn cắt Cx, Dy lần lượt tại A và B
Chứng minh:
a)AB=CA+DB
b)gócAOB=90 độ
c)Tìm độ dài đoạn thẳng BD, biết R=8cm và khi CA=4cm
GIẢI HỘ OANH VỚI Ạ HUHU!!!
Cho đường tròn ( O) có đường kính CD = 2R. Vẽ hai tiếp tuyến Cx, Dy với đường tròn. Qua K bất kì trên đường tròn (O) (K khác C, D )vẽ tiếp tuyến thứ ba với đường tròn cắt Cx, Dy lần lượt tại M, N. Gọi E là giao điểm của DK và Cx.
a) Chứng minh: MC + ND = MN và CK ^ DE ?
b) Kẻ KH vuông CD. Chứng minh : CH.CD=KD.KE
c) Chứng minh: CM.DN = R² và tính MON.
Bài 11:
Cho nửa đường tròn tâm O đường kính C . Gọi Cx, Dy là các tia vuông góc với CD (Cx,Dy và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ CD). Qua M thuộc nửa đường tròn (M khác C và D), kẻ tiếp tuyến với nửa đường tròn nó cắt Cx và Dy theo thứ tự ở A và B. Chứng minh rằng:
A,Góc AOB=9O độ
B, AB = CA+DB
C, Tính CA.DB ko đổi khi điểm M di chuyển trên nửa đường tròn
SOS
cho nửa đường tròn tam o đường kính cd= 2r từ điểm c vẽ tiếp tuyến cx của nửa đường tròn, lấy điểm m thuộc nửa đường tròn. kẻ tia dm cắt cx tại e ( e là giao điểm) kẻ mh vuông góc cd tại h....
chứng minh
a) tam giác dcm là tam giác gì vì sao
b) Md.ED=4r2
c) ch.cd = me.md
Cho nửa đường tròn tâm (o) đường kính CD à điểm I bất kì trên nửa đường tròn (i khác c,d ) kẻ tiếp tuyến Cx của nửa đường tròn cắt tia DI tại K tia phân giác của góc KCI cắt nửa đường tròn tại N cắt DK tại H tia DN cắt CI tại M cắt tia Cx tại G.
a) chứng minh các điểm H I M N cùng thuộc đường tròn và CN^2=GN.ND
1) Cho đường tròn tâm O đường kính AB. Từ A và B vẽ 2 dây AC và BD cắt nhau tại N. 2 tiếp tuyến Cx, Dy của đường tròn cắt nhau tại M. P là giao điểm 2 đường thẳng AD và BC. Chứng minh:
a) \(PN⊥AB\)
b) P, M, N thẳng hàng.
2) Cho tam giác ABC vuông ở A, đường cao AH. Đường tròn đường kính AH cắt AB, AC lần lượt tại E và F.
Chứng minh \(EF^3=EB.BC.CF\)
3) Cho nửa đường tròn đường kính AB và tiếp tuyến Ax cùng phía với nửa đường tròn đối với AB. Từ M trên Ax kẻ tiếp tuyến thứ 2 MC với nửa đường tròn, kẻ CH vuông góc với AB. CMR: MB đi qua trung điểm CH.
Cho đường tròn tâm ( O ) đường kính AB. Kẻ tiếp tuyến của nửa đường tròn. Qua điểm M bất kì thuộc đường tròn ( M khác A và B ) kẻ tiếp tuyến với nửa đường tròn cắt Ax, By thứ tự tại C, D. Chứng minh rằng:
a) ∠COD = 90 độ
b) CD = AC + BD
c) Tích AC.BD không đổi khi M di chuyển trên nửa đường tròn
Cho đường tròn tâm ( O ) đường kính AB. Kẻ tiếp tuyến của nửa đường tròn. Qua điểm M bất kì thuộc đường tròn ( M khác A và B ) kẻ tiếp tuyến với nửa đường tròn cắt Ax, By thứ tự tại C, D. Chứng minh rằng:
a) ∠COD = 90 độ
b) CD = AC + BD
c) Tích AC.BD không đổi khi M di chuyển trên nửa đường tròn
