Dựa vào một số giới hạn đặc biệt ta có:
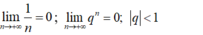
⇒ Mệnh đề C là đúng.
Chọn C.
Dựa vào một số giới hạn đặc biệt ta có:
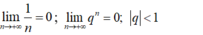
⇒ Mệnh đề C là đúng.
Chọn C.
Với k là số nguyên dương bất kỳ, xét các mệnh đề sau:
1. lim x → + ∞ 1 x k = + ∞
2 . lim x → - ∞ 1 x k = 0 3 . lim x → + ∞ x k = + ∞ 4 . lim x → - ∞ x k = + ∞ n ế u k c h ẵ n 5 . lim x → - ∞ x k = 0 n ế u k l ẻ
Số mệnh đề đúng là:
A.2
B.3
C.4
D.5
Giúp em với ạ
a) lim n (\(\sqrt{n^2+2}-n\))
b) lim \(\sqrt{n^2+2n}-n-1\)
c) lim \(\frac{1}{\sqrt{n^2+3n}-n}\)
d) lim \(\sqrt[3]{n^3+2}-n\)
e) lim \(\sqrt[3]{n^3+1}-\sqrt{n^2+n}\)
Xét các mệnh đề sau
(I). l i m n k = + ∞ với k là số nguyên dương tùy ý.
(II). lim x → ∞ 1 x k = 0 với k là số nguyên dương tùy ý.
(III). lim x → - ∞ x k = + ∞ với k là số nguyên dương tùy ý.
Trong 3 mệnh đề trên thì
A. Cả (I), (II), (III) đều đúng.
B. Chỉ (I) đúng
C. Chỉ (I),(II) đúng
D. Chỉ (III) đúng
Cho dãy số ( x n ) xác định bởi x 1 = 2 , x n + 1 = 2 + x n , n ∈ N. Mệnh đề nào là mệnh đề đúng ?
![]()
![]()
![]()
![]()
Kí hiệu C n k là số tổ hợp chập k của n phần tử (0 ≤ k ≤ n). Mệnh đề nào sau đây đúng?
A . C n k = n ! ( n - k ) !
B . C n k = n ! k !
C . C n k = n ! k ! ( n - k ) !
D . C n k = n ! k ! ( n - k ) !
Câu 1: Tính giới hạn
a, lim\(\dfrac{2-5^{n-2}}{3^n=2.5^n}\) b,lim\(\dfrac{2-5^{n+2}}{3^n-2.5^n}\)
Câu 2 :CMR :\(x^4+x^3-3x^2+x+1=0\) có ít nhất một nghiệm âm lớn hơn -1
Câu 3: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và các cạnh bên đều bằng a. Gọi M,N lần lượt là trung điểm của AD và SD. Tìm số đo góc giữa 2 đường thẳng MN và SC
7/ lim \(\sqrt{n^2+4n+1}-n\)
8/ lim \(n-\sqrt{n^2+9n-1}\) (pp liên hợp lim \(\dfrac{n^2-\left(n^2+9n-1\right)}{n+\sqrt{n^2+9n-1}}\)
9/ lim \(\dfrac{1+2+3+...+n}{n^2-1}\)
1/ lim \(\dfrac{\sqrt{n^4-n^2}+3n^2}{1-n^2}\)
2/ lim \(\dfrac{n\sqrt{n}-n^3}{4n^3+\sqrt{n}}\)
3/ lim \(\dfrac{3.4^n-1}{2.3^n+4}\)
4/ lim \(\dfrac{2^{n+1}+4.3^{n-1}}{1-2^{n-1}+3^{n+1}}\)
Hãy xem trong lời giải của bài toán sau đây có bước nào bị sai?
Bài toán: chứng minh rằng với mọi số nguyên dương n, mệnh đề sau đây đúng:
A(n) : “nếu a và b là những số nguyên dương mà max{a,b} = n thì a = b”
Chứng minh :
Bước 1: A(1):”nếu a,b là những số nguyên dương mà max{a,b} = 1 thì a = b”
Mệnh đề A(1) đúng vì max{a,b} = 1 và a,b là những số nguyên dương thì a= b =1.
Bước 2: giả sử A(k) là mệnh đề đúng vơi k≥1
Bước 3: xét max{a,b} = k+1 ⇒max{a-1,b-1} = k+ 1-1 = k
Do a(k) là mệnh đề đúng nên a- 1= b-1 ⇒ a= b⇒ A(k+1) đúng.
Vậy A(n) đúng với mọi n ∈N*
A. Bước 1
B. Bước 2
C. Bước 3
D. Không có bước nào sai
lim\(\sqrt{n^4-n^2+1}\)+2n2
lim\(\sqrt{n^4-n^2+1}\)-2n2