Ôn tập HKI
Bài 1: Tính
A = \(2\sqrt{5}-\sqrt{20}+3\sqrt{45}\)
B = \(1\sqrt{\left(2-\sqrt{3}\right)^2}+\sqrt{\left(2+\sqrt{3}\right)^2}\)
Bài 2 : Giải các phương trình
a) \(\sqrt{3x-2}=5\)
b) \(\sqrt{4x^2-4x+1}=1\)
Bài 3 : Cho 2 hàm số
(d₁): y = \(\dfrac{1}{2}x\)
(d₂): y = \(-x+3\)
a) Vẽ đồ thị của 2 hàm số trên trong cùng 1 mặt phẳng tọa độ Oxy.
b) Tìm tọa độ giao điểm của 2 đường thẳng trên bằng phép tính.
c) Viết phương trình đường thẳng (d) biết (d) song song (d₂) và cắt (d₁) tại điểm M có hoành độ là 4.
Bài 3:
a: 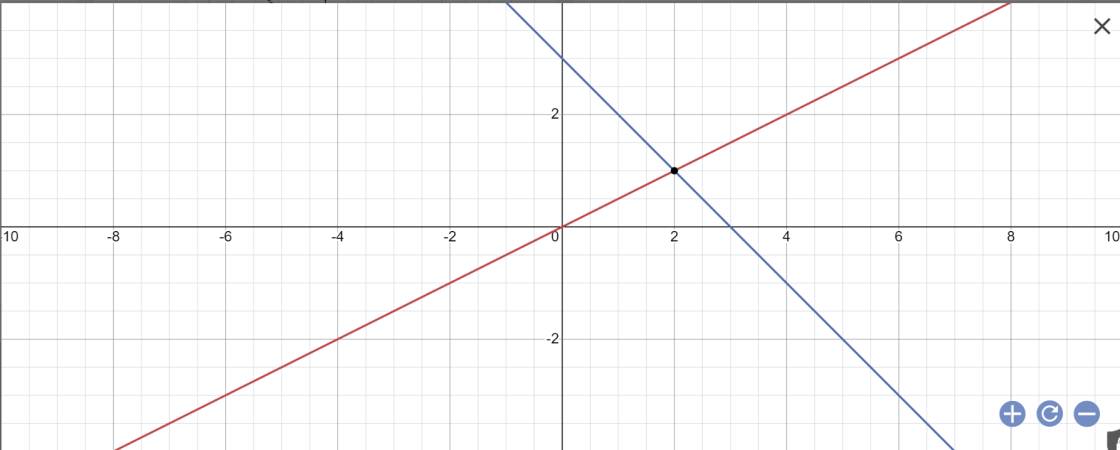
b: Phương trình hoành độ giao điểm của (d1) và (d2) là:
\(\dfrac{1}{2}x=-x+3\)
=>\(\dfrac{1}{2}x+x=3\)
=>1,5x=3
=>x=2
Khi x=2 thì y=-x+3=-2+3=1
Vậy: (d1) cắt (d2) tại A(2;1)
c:
Đặt (d): y=ax+b(a<>0)
Vì (d)//(d2) nên a=-1 và b<>3
=>(d): y=-x+b
Thay x=4 vào (d1), ta được:
\(y=\dfrac{1}{2}\cdot4=2\)
Thay x=4 và y=2 vào (d), ta được:
b-4=2
=>b=6
Vậy: (d): y=-x+6
Bài 2:
a: ĐKXĐ: x>=2/3
\(\sqrt{3x-2}=5\)
=>\(3x-2=5^2=25\)
=>3x=25+2=27
=>x=27/3=9(nhận)
b: ĐKXĐ: \(x\in R\)
\(\sqrt{4x^2-4x+1}=1\)
=>\(\sqrt{\left(2x-1\right)^2}=1\)
=>|2x-1|=1
=>\(\left[{}\begin{matrix}2x-1=1\\2x-1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=2\\2x=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=1\left(nhận\right)\\x=0\left(nhận\right)\end{matrix}\right.\)
Bài 1:
\(A=2\sqrt{5}-\sqrt{20}+3\sqrt{45}\)
\(=2\sqrt{5}-2\sqrt{5}+3\cdot3\sqrt{5}\)
\(=9\sqrt{5}\)
\(B=\sqrt{\left(2-\sqrt{3}\right)^2}+\sqrt{\left(2+\sqrt{3}\right)^2}\)
\(=\left|2-\sqrt{3}\right|+\left|2+\sqrt{3}\right|\)
\(=2-\sqrt{3}+2+\sqrt{3}=4\)










