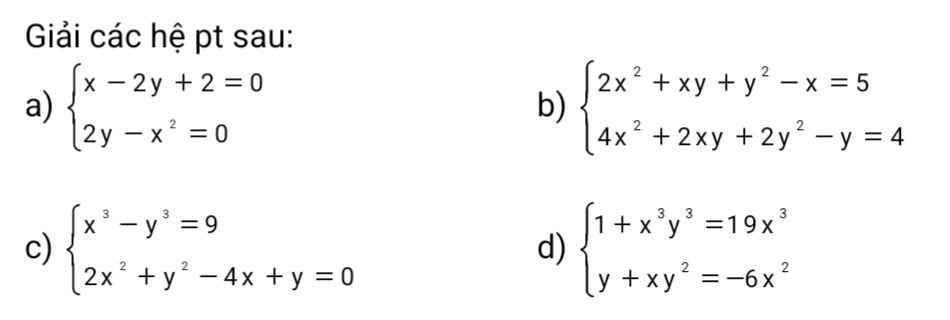a: \(\left\{{}\begin{matrix}x-2y+2=0\\2y-x^2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2y=x+2\\2y=x^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x^2=x+2\\x^2=2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-x-2=0\\y=\dfrac{x^2}{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(x-2\right)\left(x+1\right)=0\\y=\dfrac{x^2}{2}\end{matrix}\right.\)
(x-2)(x+1)=0
=>\(\left[{}\begin{matrix}x-2=0\\x+1=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Khi x=2 thì \(y=\dfrac{x^2}{2}=\dfrac{2^2}{2}=\dfrac{4}{2}=2\)
Khi x=-1 thì \(y=\dfrac{x^2}{2}=\dfrac{\left(-1\right)^2}{2}=\dfrac{1}{2}\)
b: \(\left\{{}\begin{matrix}2x^2+xy+y^2-x=5\\4x^2+2xy+2y^2-y=4\end{matrix}\right.\)(I)
=>\(\left\{{}\begin{matrix}4x^2+2xy+2y^2-2x=10\\4x^2+2xy+2y^2-y=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2x+y=6\\2x^2+xy+y^2-x=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=2x+6\\2x^2+x\left(2x+6\right)+\left(2x+6\right)^2-x=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=2x+6\\2x^2+2x^2+6x+4x^2+24x+36-x=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=2x+6\\8x^2+29x+31=0\end{matrix}\right.\)
\(8x^2+29x+31=0\)(1)
\(\text{Δ}=29^2-4\cdot8\cdot31\)
\(=841-32\cdot31=-151< 0\)
=>Phương trình (1) vô nghiệm
Do đó: Hệ phương trình (I) vô nghiệm