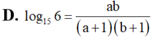Các câu hỏi tương tự
Để tính
∫
x
2
.
cos
x
.
d
x
theo phương pháp tính nguyên hàm từng phần, ta đặt: A.
u
x
d
v
x
cos
x
d...
Đọc tiếp
Để tính ∫ x 2 . cos x . d x theo phương pháp tính nguyên hàm từng phần, ta đặt:
A. u = x d v = x cos x d x
B. u = x 2 d v = cos x d x
C. u = cos x d v = x 2 d x
D. u = x 2 cos x d v = d x
Đặt
log
4
6
t
Tính
log
3
12
theo t.
Đọc tiếp
Đặt log 4 6 = t Tính log 3 12 theo t.
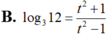
Đặt
t
log
4
x
. Tính
log
4
log
x
2
theo t.
Đọc tiếp
Đặt t = log 4 x . Tính log 4 log x 2 theo t.
Để tính
∫
xln
(
2
+
x
)
.
dx
theo phương pháp tính nguyên hàm từng phần, ta đặt: A.
u
v
d
v
ln
2...
Đọc tiếp
Để tính ∫ xln ( 2 + x ) . dx theo phương pháp tính nguyên hàm từng phần, ta đặt:
A. u = v d v = ln 2 + x d x
B. u = ln 2 + x d v = x d x
C. u = x ln 2 + x d v = d x
D. u = ln 2 + x d v = d x
Để tính
∫
x
ln
(
2
+
x
)
d
x
theo phương pháp tính nguyên hàm từng phần, ta đặt: A.
u
v
d
v
ln
2...
Đọc tiếp
Để tính ∫ x ln ( 2 + x ) d x theo phương pháp tính nguyên hàm từng phần, ta đặt:
A. u = v d v = ln 2 + x d x
B. u = ln 2 + x d v = x d x
C. u = x ln 2 + x d v = d x
D. u = ln 2 + x d v = d x
Đặt
t
2
-
3
x
. Tính
7
+
4
3
x
theo t.
Đọc tiếp
Đặt t = 2 - 3 x . Tính 7 + 4 3 x theo t.
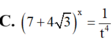
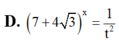
Đặt a= log23 . Hãy tính log2 48 theo a
A. 3+ 2a
B. 4+ 2a
C. 4+ a
D. 5- a
Đặt
a
log
2
3
,
b
log
5
6
. Tính
log
15
6
theo a, b
Đọc tiếp
Đặt a = log 2 3 , b = log 5 6 . Tính log 15 6 theo a, b
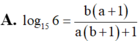
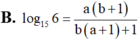
Tính các tích phân sau: ∫ 0 1 y - 1 2 y d y , đặt t = y