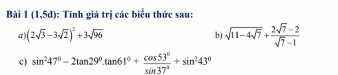1: \(A=-3\sqrt{12}+\sqrt{75}+\sqrt{\left(1-\sqrt{3}\right)^2}+\dfrac{1}{\sqrt{3}-2}\)
\(=-6\sqrt{3}+5\sqrt{3}+\sqrt{3}-1-\dfrac{1}{2-\sqrt{3}}\)
\(=-1-\dfrac{\left(2+\sqrt{3}\right)}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}\)
\(=-1-2-\sqrt{3}=-3-\sqrt{3}\)
2:
a: \(P=\left(\dfrac{x+2}{\sqrt{x}+1}-\sqrt{x}\right):\left(\dfrac{\sqrt{x}-4}{1-x}-\dfrac{\sqrt{x}}{\sqrt{x}+1}\right)\)
\(=\dfrac{x+2-\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}+1}:\left(\dfrac{-\sqrt{x}+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}}{\sqrt{x}+1}\right)\)
\(=\dfrac{-\sqrt{x}+2}{\sqrt{x}+1}:\dfrac{-\sqrt{x}+4-\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{-\sqrt{x}+2}{\sqrt{x}+1}\cdot\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{-\sqrt{x}+4-x+\sqrt{x}}\)
\(=\dfrac{-\sqrt{x}+2}{1}\cdot\dfrac{\sqrt{x}-1}{-x+4}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\)
b: \(P-1=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}-1=\dfrac{\sqrt{x}-1-\sqrt{x}-2}{\sqrt{x}+2}=\dfrac{-3}{\sqrt{x}+2}< 0\)
=>P<1


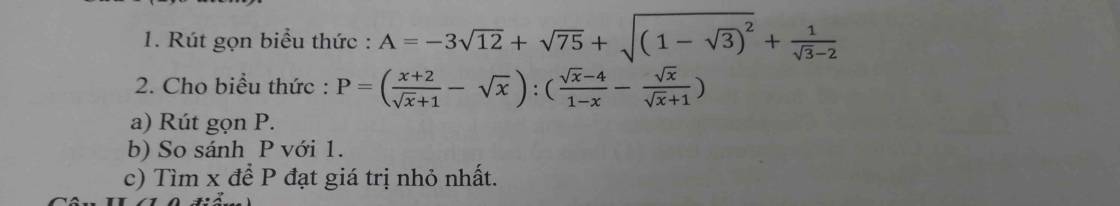






 nhanh nh
nhanh nh