Các câu hỏi tương tự
Cho hàm số
f
(
x
)
a
x
4
+
b
x
2
+
c
với a0, c2018 và a+b+c2018. Số điểm cực trị của hàm số
y
f
(
x
)
-
2018
là A. 1 B. 3 C. 5 D. 7
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 2 + c với a>0, c>2018 và a+b+c<2018. Số điểm cực trị của hàm số y = f ( x ) - 2018 là
A. 1
B. 3
C. 5
D. 7
Cho hàm số f(x) có f ' ( x ) = x 2017 ( x - 1 ) 2018 ( x + 1 ) 2018 , ∀ x ∈ ℝ . Hỏi hàm số đã cho có bao nhiêu điểm cực trị?
A. 0
B. 1
C. 2
D. 3
Cho hàm số f(x) có đạo hàm trên
ℝ
thỏa mãn f’(x) – 2018f(x) 2018.x2017.e2018x với mọi
x
∈
ℝ
và f(0) 2018. Tính giá trị f(1). A. f(1) 2019e2018. B. f(1) 2018e-2018. C. f(1) 2018e2018. D. f(1) 2017e2018.
Đọc tiếp
Cho hàm số f(x) có đạo hàm trên ℝ thỏa mãn f’(x) – 2018f(x) = 2018.x2017.e2018x với mọi x ∈ ℝ và f(0) = 2018. Tính giá trị f(1).
A. f(1) = 2019e2018.
B. f(1) = 2018e-2018.
C. f(1) = 2018e2018.
D. f(1) = 2017e2018.
hàm số
f
(
x
)
ln
1
-
1
x
2
. Biết rằng
f
(
2
)
+
F
(
3
)
+
.
.
.
+
f
(
2018
)
ln
a
-
ln
b...
Đọc tiếp
hàm số f ( x ) = ln 1 - 1 x 2 . Biết rằng f ( 2 ) + F ( 3 ) + . . . + f ( 2018 ) = ln a - ln b + ln c - ln d với a, b, c, d là các số nguyên dương, trong đó a, c, d là các số nguyên tố và a<b<c<d. Tính P=a+b+c+d
A. 1986
B. 1698
C. 1689
D. 1968
Cho hàm số
f
(
x
)
x
2
1
-
x
. Đạo hàm cấp 2018 của hàm số f(x) là:
Đọc tiếp
Cho hàm số f ( x ) = x 2 1 - x . Đạo hàm cấp 2018 của hàm số f(x) là:
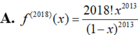
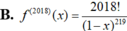
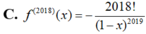
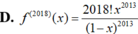
Biết F(x) làm một nguyên hàm của hàm số
f
(
x
)
2016
.
e
2016
và F(0) 2018. Giá trị của F(1) là A. F(1) 2016 B.
F
(
1
)
2016
e
2016
C.
F
(
1
)
2016
e...
Đọc tiếp
Biết F(x) làm một nguyên hàm của hàm số f ( x ) = 2016 . e 2016 và F(0) = 2018. Giá trị của F(1) là
A. F(1) = 2016
B. F ( 1 ) = 2016 e 2016
C. F ( 1 ) = 2016 e 2016 + 2
D. F ( 1 ) = e 2016 + 2017
Cho hàm số f(x)= x(x-1)(x-2) (x-3)... (x-2018).
Tính f'(1)
A. -2017!
B. 0
C. 2017!
D. 2018
Cho hàm số f(x) có đạo hàm trên R thỏa mãn f(x)-2018f(x)
2018
x
2017
e
2018
x
với mọi
x
∈
ℝ
, f(0)2018. Tính f(1)
Đọc tiếp
Cho hàm số f(x) có đạo hàm trên R thỏa mãn f'(x)-2018f(x)= 2018 x 2017 e 2018 x với mọi x ∈ ℝ , f(0)=2018. Tính f(1)
![]()
![]()
![]()
![]()
Hàm số f(x) có đạo hàm f (x) trên R. Hình vẽ bên là đồ thị của hàm số f (x) trên R. Hỏi hàm số
y
f
(
|
x
|
)
+
2018
có bao nhiêu điểm cực trị? A.5 B.3 C.2 D.4
Đọc tiếp
Hàm số f(x) có đạo hàm f '(x) trên R. Hình vẽ bên là đồ thị của hàm số f '(x) trên R.
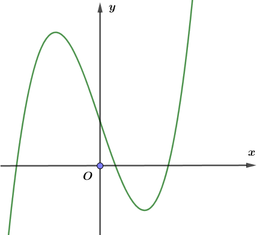
Hỏi hàm số y = f ( | x | ) + 2018 có bao nhiêu điểm cực trị?
A.5
B.3
C.2
D.4
Cho hàm số
f
(
x
)
a
x
4
+
b
x
2
-
1
(
a
,
b
∈
ℝ
)
. Đồ thị của hàm số yf(x) như hình vẽ bên. Số nghiệm thực của phương trình 2018.f(x) + 2019 0 là: A. 4 B. 0 C. 3 D. 2
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 2 - 1 ( a , b ∈ ℝ ) . Đồ thị của hàm số y=f(x) như hình vẽ bên. Số nghiệm thực của phương trình 2018.f(x) + 2019 = 0 là:
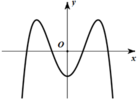
A. 4
B. 0
C. 3
D. 2



