21 tháng 8 lúc 21:04
Các câu hỏi tương tự
Hãy nhắc lại:
a) Các hằng đẳng thức lượng giác cơ bản;
b) Công thức cộng;
c) Công thức nhân đôi;
d) Công thức biến đổi tích thành tổng và tổng thành tích.
Chứng minh công thức tính diện tích tổng quát của đa giác đều có số cạnh là n. Từ đó suy ra công thức tính diện tích hình tròn.
Biến đổi biểu thức sin a + 1 thành tích.
29 tháng 7 2023 lúc 14:26
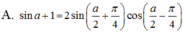
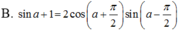
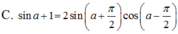
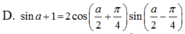
Biến đổi thành tích biểu thức B= cos2x + cosx -sin x
Cho mặt cầu (S) có tâm O và bán kính R. Diện tích mặt cầu (S) được cho bởi công thức nào trong các công thức dưới đây?
A
.
4
πR
2
B
.
4
R
2
C
.
4
3
πR
2
D
.
πR
2
Đọc tiếp
Cho mặt cầu (S) có tâm O và bán kính R. Diện tích mặt cầu (S) được cho bởi công thức nào trong các công thức dưới đây?
A . 4 πR 2
B . 4 R 2
C . 4 3 πR 2
D . πR 2
Cho
k
∈
ℕ
,
n
∈
ℕ
. Trong các công thức về số các chỉnh hợp và số các tổ hợp sau, công thức nào là công thức đúng? A.
C
n
k
n
!
(
n
-
k
)
!
với...
Đọc tiếp
Cho k ∈ ℕ , n ∈ ℕ . Trong các công thức về số các chỉnh hợp và số các tổ hợp sau, công thức nào là công thức đúng?
A. C n k = n ! ( n - k ) ! với 0 ≤ k ≤ n
B. A n k = n ! k ! ( n - k ) ! với 0 ≤ k ≤ n
C. C n + 1 k = C n k + C n k - 1 với 1 ≤ k ≤ n
D. C n + 1 k = C n k + 1 với 0 ≤ k ≤ n - 1
Phát biểu định nghĩa cấp số cộng và công thức tính tổng n số hạng đầu tiên của một số không đổi d.
Dùng công thức cộng,công thức nhân đôi hạ bậc tính giá trị của biểu thức sau(ko dùng mt) A=cos36°×cos72°
Trong các công thức sau, công thức nào đúng?
A
.
C
n
k
A
n
k
k
B
.
A
n
k
n
!
(
n
-...
Đọc tiếp
Trong các công thức sau, công thức nào đúng?
A . C n k = A n k k
B . A n k = n ! ( n - k ) !
C . C n k = n ! k ( n - k ) !
D . A n k = n ! ( n - k )
Cho cấp số nhân lùi vô hạn
u
n
có công bội q. Khi đó tổng của cấp số nhân lùi vô hạn đó được tính bởi công thức nào sau đây: A.
S
1
1
-
q
B.
S
u
1
1
-
q
C.
S...
Đọc tiếp
Cho cấp số nhân lùi vô hạn u n có công bội q. Khi đó tổng của cấp số nhân lùi vô hạn đó được tính bởi công thức nào sau đây:
A. S = 1 1 - q
B. S = u 1 1 - q
C. S = u 1 1 + q n
D. S = u 1 1 - q n