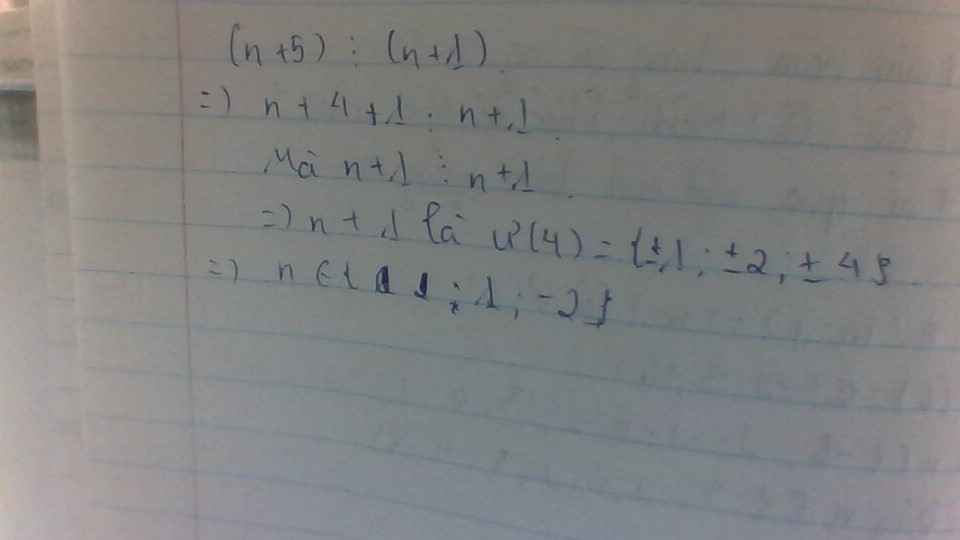\(\left(n+5\right)⋮\left(n+1\right)\)
\(\Rightarrow\left(n+1\right)+4⋮\left(n+1\right)\)
\(\Rightarrow4⋮\left(n+1\right)\Rightarrow\left(n+1\right)\inƯ\left(4\right)=\left\{1;-1;2;-2;4;-4\right\}\)
Do \(n\in N\)
\(\Rightarrow n\in\left\{0;1;3\right\}\)
(n+5)⋮(n+1)(n+5)⋮(n+1)
⇒(n+1)+4⋮(n+1)⇒(n+1)+4⋮(n+1)
⇒4⋮(n+1)⇒(n+1)∈Ư(4)={1;−1;2;−2;4;−4}⇒4⋮(n+1)⇒(n+1)∈Ư(4)={1;−1;2;−2;4;−4}
Do n∈Nn∈N
⇒n∈{0;1;3}
Ta có: \(n+5⋮n+1\)
\(\Leftrightarrow n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{0;-2;1;-3;3;-5\right\}\)