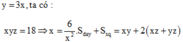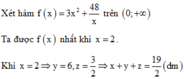Các câu hỏi tương tự
Một xưởng sản xuất những thùng bằng kẽm hình hộp chữ nhật không có nắp và có các kích thước x,y,z (dm). Biết tỉ số hai cạnh đáy là
x
:
y
1
:
3
và thể tích của hộp bằng
18
(
d
m
3
)
. Để tốn ít vật liệu nhất thì tổng
x
+
y
+
z
bằng? A.
26
3
B. 10 C. ...
Đọc tiếp
Một xưởng sản xuất những thùng bằng kẽm hình hộp chữ nhật không có nắp và có các kích thước x,y,z (dm). Biết tỉ số hai cạnh đáy là x : y = 1 : 3 và thể tích của hộp bằng 18 ( d m 3 ) . Để tốn ít vật liệu nhất thì tổng x + y + z bằng?
A. 26 3
B. 10
C. 19 2
D. 26
Một xưởng sản xuất những thùng bằng kẽm hình hộp chữ nhật không có nắp và có các kích thước x, ỵ, z (dm). Biết tỉ số hai cạnh đáy là x:y1:3, thể tích của khối hộp bằng 18 lít. Để tốn ít vật liệu nhất thì bộ số x, ỵ, z là. A.
x
2
,
y
6
,
z
3
2
B.
x
1
,
y
3
,
...
Đọc tiếp
Một xưởng sản xuất những thùng bằng kẽm hình hộp chữ nhật không có nắp và có các kích thước x, ỵ, z (dm). Biết tỉ số hai cạnh đáy là x:y=1:3, thể tích của khối hộp bằng 18 lít. Để tốn ít vật liệu nhất thì bộ số x, ỵ, z là.
A. x = 2 , y = 6 , z = 3 2
B. x = 1 , y = 3 , z = 6
C. x = 3 2 , y = 9 2 , z = 3 2
D. x = 1 2 , y = 3 2 , z = 24
Một người thợ cơ khí cần gò một chiếc thùng bằng tôn cứng, thùng có dạng hình hộp chữ nhật không có nắp và kích cỡ các chiều là x, y, z (dm) đồng thời tỉ lệ x/y1/3, thể tích của thùng là 18 lít. Hỏi số tiền ít nhất mà người thợ phải bỏ ra để mua tôn là bao nhiêu, biết rằng mỗi đềximét vuông tôn có giá 20 nghìn đồng A. 720 nghìn B. 820 nghìn C. 620 nghìn D. 920 nghìn
Đọc tiếp
Một người thợ cơ khí cần gò một chiếc thùng bằng tôn cứng, thùng có dạng hình hộp chữ nhật không có nắp và kích cỡ các chiều là x, y, z (dm) đồng thời tỉ lệ x/y=1/3, thể tích của thùng là 18 lít. Hỏi số tiền ít nhất mà người thợ phải bỏ ra để mua tôn là bao nhiêu, biết rằng mỗi đềximét vuông tôn có giá 20 nghìn đồng
A. 720 nghìn
B. 820 nghìn
C. 620 nghìn
D. 920 nghìn
Công ty A cần xây bể chứa hình hộp chữ nhật (không có nắp), đáy là hình vuông cạnh bằng a(m), chiều cao bằng h(m). Biết thể tích bể chứa cần xây bằng 62,5 m3, hỏi kích thước cạnh đáy và chiều cao bằng bao nhiêu để tổng diện tích các mặt xung quanh và mặt đáy nhỏ nhất? D. a 5m, h 2,5m
Đọc tiếp
Công ty A cần xây bể chứa hình hộp chữ nhật (không có nắp), đáy là hình vuông cạnh bằng a(m), chiều cao bằng h(m). Biết thể tích bể chứa cần xây bằng 62,5 m3, hỏi kích thước cạnh đáy và chiều cao bằng bao nhiêu để tổng diện tích các mặt xung quanh và mặt đáy nhỏ nhất?
![]()
![]()
![]()
D. a = 5m, h = 2,5m
Người ta muốn thiết kế một bế cá bằng kính không có nắp với thể tích là
80
dm
3
và chiều cao là 4dm. Đặt một vách ngăn có cùng bán kính ở giữa, chia bể thành hai ngăn, với các kích thước là x,y (dm) như hình vẽ. Tính x,y đế bể cá tốn ít nguyên liệu nhất (tính cả tấm kính ngăn ở giữa), coi bề dày các tâm kính là như nhau và không ảnh hưởng đến thể tích của bể. A.
x
4
,
y...
Đọc tiếp
Người ta muốn thiết kế một bế cá bằng kính không có nắp với thể tích là 80 dm 3 và chiều cao là 4dm. Đặt một vách ngăn có cùng bán kính ở giữa, chia bể thành hai ngăn, với các kích thước là x,y (dm) như hình vẽ. Tính x,y đế bể cá tốn ít nguyên liệu nhất (tính cả tấm kính ngăn ở giữa), coi bề dày các tâm kính là như nhau và không ảnh hưởng đến thể tích của bể.
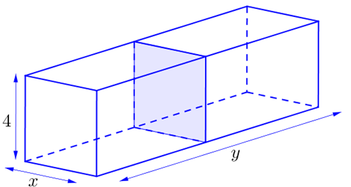
A. x = 4 , y = 5
B. x = 2 30 3 , y = 30
C. x = 2 5 , y = 2 5
D. x = 4 15 3 , y = 15
Một cái hộp không nắp được làm từ một miếng bìa các tông theo mẫu ở hình vẽ bên. Hộp có đáy là một hình vuông cạnh x (cm), chiều cao h (cm) và thể tích của hộp là
500
c
m
3
. Tìm x để nguyên liệu làm hộp tốn ít nhất. A. x8 B. x5 C. x10 D. x12
Đọc tiếp
Một cái hộp không nắp được làm từ một miếng bìa các tông theo mẫu ở hình vẽ bên. Hộp có đáy là một hình vuông cạnh x (cm), chiều cao h (cm) và thể tích của hộp là 500 c m 3 . Tìm x để nguyên liệu làm hộp tốn ít nhất.
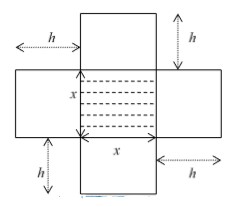
A. x=8
B. x=5
C. x=10
D. x=12
Một xưởng sản xuất cần làm 100 chiếc hộp inox bằng nhau, hình dạng là hình hộp chữ nhật có đáy là hình vuông (họp không có nắp), với thể tích là
108
d
m
3
/
1
h
ộ
p
. Giá inox là
47
.
000
đ
ồ
n
g
/
1
d
m
2
. Hãy tính toán sao cho tổng tiền chi phí cho 100 chiếc hộp là ít nhất...
Đọc tiếp
Một xưởng sản xuất cần làm 100 chiếc hộp inox bằng nhau, hình dạng là hình hộp chữ nhật có đáy là hình vuông (họp không có nắp), với thể tích là 108 d m 3 / 1 h ộ p . Giá inox là 47 . 000 đ ồ n g / 1 d m 2 . Hãy tính toán sao cho tổng tiền chi phí cho 100 chiếc hộp là ít nhất, và số tiền tối thiểu đó là bao nhiêu (nếu chỉ tính số inox vừa đủ để sản xuất 100 chiếc hộp, không có phần dư thừa, cắt bỏ)?
A. 1.692.000.000 đồng
B. 507.666.000 đồng
C. 1.015.200.000 đồng
D. 235.800.000 đồng
Người ta thiết kế một thùng chứa hình trụ có thể tích V cho trước. Biết rằng đơn giá của vật liệu làm mặt đáy và nắp của thùng bằng nhau và gấp 3 lần so với đơn giá vật liệu để làm mặt xung quanh của thùng (chi phí cho mỗi đơn vị diện tích). Gọi chiều cao của thùng là h và bán kính đáy là r. Tính tỉ số
h
r
sao cho chi phí vật liệu sản xuất thùng là nhỏ nhất? A.
h
r...
Đọc tiếp
Người ta thiết kế một thùng chứa hình trụ có thể tích V cho trước. Biết rằng đơn giá của vật liệu làm mặt đáy và nắp của thùng bằng nhau và gấp 3 lần so với đơn giá vật liệu để làm mặt xung quanh của thùng (chi phí cho mỗi đơn vị diện tích). Gọi chiều cao của thùng là h và bán kính đáy là r. Tính tỉ số h r sao cho chi phí vật liệu sản xuất thùng là nhỏ nhất?
A. h r = 2
B. h r = 2
C. h r = 6
D. h r = 3 2
Người ta thiết kế một thùng chứa hình trụ (như hình vẽ) có thể tích V không đổi. Biết rằng giá của vật liệu làm mặt đáy và nắp của thùng bằng nhau và đắt gấp 3 lần so với giá vật liệu để làm mặt xung quanh của thùng (chi phí cho mỗi đơn vị diện tích). Gọi chiều cao của thùng là h và bán kính đáy là r . Tính tỷ số
h
r
sao cho chi phí vật liệu sản xuất thùng nhỏ nhất. A.
h
r
1 B.
h...
Đọc tiếp
Người ta thiết kế một thùng chứa hình trụ (như hình vẽ) có thể tích V không đổi. Biết rằng giá của vật liệu làm mặt đáy và nắp của thùng bằng nhau và đắt gấp 3 lần so với giá vật liệu để làm mặt xung quanh của thùng (chi phí cho mỗi đơn vị diện tích). Gọi chiều cao của thùng là h và bán kính đáy là r . Tính tỷ số h r sao cho chi phí vật liệu sản xuất thùng nhỏ nhất.
A. h r = 1
B. h r = 2
C. h r = 6
D. h r = 9