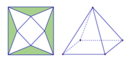
Một sợi dây có chiều dài L (m) được chia thành ba phần. Phần thứ nhất được uốn thành hình vuông, phần thứ hai được uốn thành tam giác đều có cạnh gấp hai lần cạnh của hình vuông, phần thứ ba được uốn thành hình tròn (như hình vẽ).

Hỏi độ dài cạnh hình tam giác đều bằng bao nhiêu để tổng diện tích 3 hình thu được là nhỏ nhất?
A. 7 L 49 + 3 + 1 π m
B. 5 L 49 + 3 + 1 π m
C. 5 L 25 + 3 + 1 π m
D. 7 L 25 + 3 + 1 π m
Chọn đáp án C
Gọi độ dài cạnh của hình vuông là x (m) thì độ dài cạnh tam giác đều là 2x (m).
Chiều dài phần dây được uống thành hình vuông (chính là chu vi hình vuông) là 4x (m); chiều dài phần dây được uốn thành tam giác đều (chính là chu vi hình tam giác đều) là 6x(m) .
Suy ra chiều dài phần dây được uốn thành hình tròn là L - 4 x - 6 x = L - 10 x ( m )
Từ đó ta có x ∈ 0 ; L 10
Gọi r là bán kính của đường tròn thì chu vi đường tròn là
![]()
Tổng diện tích của ba hình là
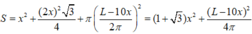
Xét hàm số
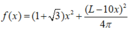
trên 0 ; L 10
Ta có

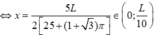
Lập bảng biến thiên ta thấy
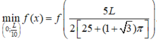
Vậy tổng diện tích của ba hình thu được nhỏ nhất khi x = 5 L 2 25 + 1 + 3 π
suy ra độ dài cạnh của tam giác đều là 2 x = 5 L 25 + 1 + 3 π