Một người cần làm một hình lăng trụ tam giác đều từ tấm nhựa phẳng để có thể tích là 6 3 c m 3 Để ít hao tốn vật liệu nhất thì cần tính độ dài các cạnh của khối lăng trụ tam giác đều này bằng bao nhiêu?
A. Cạnh đáy bằng 4 3 c m và cạnh bên bằng 1 2 c m
B. Cạnh đáy bằng 2 6 c m và cạnh bên bằng 1 c m
C. Cạnh đáy bằng 2 2 c m và cạnh bên bằng 3 c m
D. Cạnh đáy bằng 2 6 c m và cạnh bên bằng 1 c m
Đáp án A
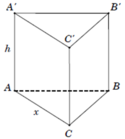
HD Giả sử hình lăng trụ tam giác đều cần làm là ABC.A'B'C' có độ dài AB = x,AA' = h
Khi đó S ∆ A B C = 3 4 x 2 và V A B C . A ' B ' C ' = S A B C . A A ' = 3 4 x 2 h
Theo giả thiết 3 4 x 2 h = 6 3 ⇒ h = 24 x 2
Để ít tốn vật liệu nhất thì diện tích toàn phần của khối lăng trụ ABC.A'B'C' là nhỏ nhất.
Gọi S t p là tổng diện tích các mặt của khối lăng trụ ABC.A'B'C' ,ta có
S t p = 2 S ∆ A B C + 3 S A B B ' A ' = 3 2 x 2 + 2 h x = 3 2 x 2 + 72 x
Khảo sát f ( x ) = 3 2 x 2 + 72 x trên ( 0 ; + ∞ ) ,ta được f (x) nhỏ nhất khi x = 2 3
Với x = 2 3 c m → h = 2 c m



