diện tích của mảnh vườn là S=36*25=900 (m vuông)
=>diện tích mảnh đất trồng hoa =1/9*900=100 (m vuông)
gọi canhj của vườn hoa là a => a*a=100
=>a=10
=>chu vi vườn hoaC=4*a=40 (m)
Một vật được ném ngang ở độ cao 45 m so với mặt đất. Bỏ qua sức cản của không khí và lấy g = 10 m/s2. Thời gian vật rơi tới khi chạm đất là
A.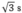 
.
B. 4,5 s.
C. 9 s.
D. 3 s.
Trong Công viên Toán học có những mảnh đất hình dáng khác nhau. Mỗi mảnh được trồng một loài hoa và nó được tạo thành bởi một trong những đường cong đẹp trong toán học. Ở đó có một mảnh đất mang tên Bernoulli, nó được tạo thành từ đường Lemniscate có phương trình trong hệ tọa độ Oxy là 16 y 2 = x 2 ( 25 - x 2 ) như hình vẽ bên. Tính diện tích S của mảnh đất Bernoulli biết rằng mỗi đơn vị trong hệ trục tọa độ Oxy tương ứng với chiều dài 1 mét.
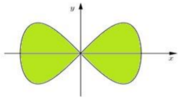
A. S = 125 6 ( m 2 )
B. S = 125 4 ( m 2 )
C. S = 250 3 ( m 2 )
D. S = 125 3 ( m 2 )
Một khu vườn hình chữ nhật có chiều dài là (hỗn số 14 một phần hai),chiều rộng bằng 3/5 chiều dài.Tính chu vi và diện tích của khu vườn đó.
Một bình đựng nước dạng hình nón (không có đáy), đựng đầy nước. Người ta thả vào đó một khối cầu không thấm nước, có đường kính bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là V. Biết rằng khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng một nửa của khối cầu chìm trong nước (hình bên).
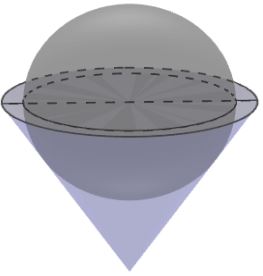
Tính thể tích nước còn lại trong bình.
A. 1 6 V
B. 1 3 V .
C. V
D. 1 π V .
Cho đa giác đều 32 cạnh. Gọi S là tập hợp các tứ giác tạo thành có 4 đỉnh lấy từ các đỉnh của đa giác đều. Chọn ngẫu nhiên một phần tử của S. Xác suất để chọn được một hình chữ nhật là
A. 1 341
B. 1 385
C. 1 261
D. 1 899
Cho hình chóp S.ABC có (SAB), (SAC) cùng vuông góc với đáy, cạnh bên SB tạo với đáy một góc 60 ° , đáy ABC là tam giác vuông cân tại B với BA=BC=a. Gọi M, N lần lượt là trung điểm của SB, SC. Tính thể tích khối đa diện AMNBC?
A. a 3 3 4
B. a 3 3 6
C. a 3 3 24
D. a 3 3 8
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a a > 0 . Hai mặt phẳng (SBC) và S C D cùng tạo với mặt phẳng (ABCD) một góc 45 ° . Biết S B = a và hình chiếu của S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính thể tích khối chóp S.ABCD
A. 2 a 3 3
B. 2 a 3 6
C. a 3 4
D. 2 a 3 9
Người ta thiết kế một bể cá bằng kính không có nắp với thể tích 72 d m 3 và có chiều cao bằng 3 dm. Một vách ngăn (cùng bằng kính) ở giữa, chia bể cá thành hai ngăn, với các kích thước a, b (đơn vị dm) như hình vẽ. Tính a, b để bể cá tốn ít nguyên liệu nhất (tính cả tấm kính ở giữa), coi bể dày các tấm kính như nhau và không ảnh hưởng đến thể tích của bể.
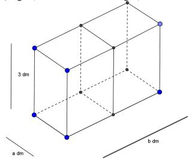
A. a= 24 , b= 21
B. a=3,b=8
C. a=3 2 , b=4 2
D. a=4,b=6
Cho hình chóp đều S.ABCD, đáy ABCD là hình vuông cạnh a, các cạnh bên tạo với đáy góc 45 độ. Diện tích toàn phần của hình chóp trên theo a là.
A. 2 3 a 2
B. 3 + 1 a 2
C. 3 - 1 a 2
D. 4 a 2
