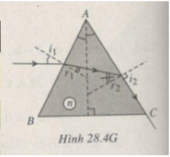
Theo đề bài: i = 30 ° ; sin r 1 = 1/2n
i 2 = 90 ° (HÌnh 28.4G); r 2 = i g h → sin r 2 = 1/n
Nhưng r 1 = A – r 2 – 60 ° - i g h
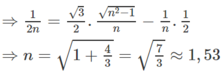
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6

Theo đề bài: i = 30 ° ; sin r 1 = 1/2n
i 2 = 90 ° (HÌnh 28.4G); r 2 = i g h → sin r 2 = 1/n
Nhưng r 1 = A – r 2 – 60 ° - i g h
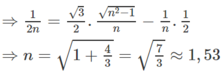
Một lăng kính có tiết diện thẳng là tam giác ABC, góc chiết quang A = 45 0 . Chiếu một tia sáng đơn sắc tới lăng kính theo phương vuông góc với mặt bên AB. Tia sáng khi đi ra khỏi lăng kính nằm sát với mặt bên AC. Chiết suất của lăng kính bằng:
A. 1,41.
B. 2,0.
C. 1,33.
D. 1,5.
Chiếu một chùm tia sáng đỏ hẹp coi như một tia sáng vào mặt bên của một lăng kính có tiết diện thẳng là tam giác cân ABC có góc chiết quang A = 8 ° theo phương vuông góc với mặt phẳng phân giác của góc chiết quang tại một điểm tới rất gần A. Biết chiết suất của lăng kính đối với tia đỏ là n d = 1 , 5 . Góc lệch của tia ló so với tia tới là:
Lăng kính thủy tinh có tiết diện thẳng là tam giác cân ABC đỉnh A. Một tia đơn sắc được chiếu vuông góc tới mặt bên AB. Sau hai lần phận toàn phần trên hai mặt AC và AB, tia ló ra khỏi đáy BC theo phương vuông góc với BC.
Vẽ đường truyền của tia sáng và tính góc chiết quang A.
Lăng kính thủy tinh có tiết diện thẳng là tam giác cân ABC đỉnh A. Một tia đơn sắc được chiếu vuông góc tới mặt bên AB. Sau hai lần phận toàn phần trên hai mặt AC và AB, tia ló ra khỏi đáy BC theo phương vuông góc với BC. Góc chiết quang A của lăng kính là
A. 30 0
B. 22 , 5 0
C. 36 0
D. 40 0
Lăng kính thủy tinh có tiết diện thẳng là tam giác cân ABC đỉnh A. Một tia đơn sắc được chiếu vuông góc tới mặt bên AB. Sau hai lần phận toàn phần trên hai mặt AC và AB, tia ló ra khỏi đáy BC theo phương vuông góc với BC. Góc chiết quang A của lăng kính là
A. 30 °
B. 22 , 5 °
C. 36 °
D. 40 °
Lăng kính thủy tinh có tiết diện thẳng là tam giác cân ABC đỉnh A. Một tia đơn sắc được chiếu vuông góc tới mặt bên AB. Sau hai lần phận toàn phần trên hai mặt AC và AB, tia ló ra khỏi đáy BC theo phương vuông góc với BC. Tìm điều kiện mà chiết suất n của lăng kính thỏa mãn.
Lăng kính thủy tinh có tiết diện thẳng là tam giác cân ABC đỉnh A. Một tia đơn sắc được chiếu vuông góc tới mặt bên AB. Sau hai lần phản xạ toàn phần trên hai mặt AC và AB, tia ló ra khỏi đáy BC theo phương vuông góc với BC. Tính góc chiết quang A:
A. 39 0
B. 36 0
C. 30 0
D. 33 0
Lăng kính có chiết suất n = 2 và góc chiết quang A = 60 0 . Một chùm tia sáng đơn sắc hẹp được chiếu vào mặt bên AB của lăng kính với góc tới . Tính góc ló của tia sáng khi ra khỏi lăng kính và góc lệch của tia ló và tia tới.
A. 20 0
B. 30 0
C. 40 0
D. 50 0
Chiếu một tia sáng đơn sắc đến mặt bên AB của một lăng kính tiết diện là một tam giác đều ABC theo phương song song với đáy BC. Tia ló ra khỏi AC đi là là mặt AC. Chiết suất của chất làm lăng kính là:
A. 2
B. 1,8
C.1,53
D. 3