Đáp án: C
Ta có:
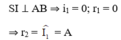
Mặt khác từ hình vẽ: SI // pháp tuyến tại J
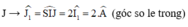
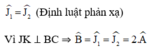
Theo tính chất góc trong của tam giác cân ABC ta có:
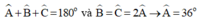
Đáp án: C

Ta có:
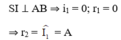
Mặt khác từ hình vẽ: SI // pháp tuyến tại J
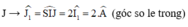
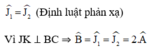
Theo tính chất góc trong của tam giác cân ABC ta có:
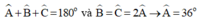
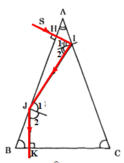
Lăng kính thủy tinh có tiết diện thẳng là tam giác cân ABC đỉnh A. Một tia đơn sắc được chiếu vuông góc tới mặt bên AB. Sau hai lần phận toàn phần trên hai mặt AC và AB, tia ló ra khỏi đáy BC theo phương vuông góc với BC. Góc chiết quang A của lăng kính là
A. 30 °
B. 22 , 5 °
C. 36 °
D. 40 °
Lăng kính thủy tinh có tiết diện thẳng là tam giác cân ABC đỉnh A. Một tia đơn sắc được chiếu vuông góc tới mặt bên AB. Sau hai lần phận toàn phần trên hai mặt AC và AB, tia ló ra khỏi đáy BC theo phương vuông góc với BC.
Vẽ đường truyền của tia sáng và tính góc chiết quang A.
Lăng kính thủy tinh có tiết diện thẳng là tam giác cân ABC đỉnh A. Một tia đơn sắc được chiếu vuông góc tới mặt bên AB. Sau hai lần phận toàn phần trên hai mặt AC và AB, tia ló ra khỏi đáy BC theo phương vuông góc với BC. Tìm điều kiện mà chiết suất n của lăng kính thỏa mãn.
Lăng kính thủy tinh có tiết diện thẳng là tam giác cân ABC đỉnh A. Một tia đơn sắc được chiếu vuông góc tới mặt bên AB. Sau hai lần phản xạ toàn phần trên hai mặt AC và AB, tia ló ra khỏi đáy BC theo phương vuông góc với BC. Tính góc chiết quang A:
A. 39 0
B. 36 0
C. 30 0
D. 33 0
Một lăng kính thủy tinh có tiết diện thẳng là tam giác ABC có góc A = 90 ° , g ó c C = 15 ° , chiết suất là n. Chiếu tia sáng đơn sắc tới mặt AB như hình bên, tia khúc xạ tới mặt BC bị phản xạ toàn phần, sau đó tới mặt AC rồi ló ra theo phương vuông góc với tia tới. Tìm các giá trị của n và α
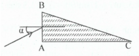
A. 2 ≤ n ≤ 2 ; 45 ° ≤ α ≤ 90 ° .
B. 3 ≤ n ≤ 2 ; 45 ° ≤ α ≤ 90 ° .
C. 2 ≤ n ≤ 2 ; 45 ° ≤ α ≤ 60 ° .
D. 3 ≤ n ≤ 2 ; 30 ° ≤ α ≤ 60 ° .
Một lăng kính có tiết diện thẳng là tam giác ABC, góc chiết quang A = 45 0 . Chiếu một tia sáng đơn sắc tới lăng kính theo phương vuông góc với mặt bên AB. Tia sáng khi đi ra khỏi lăng kính nằm sát với mặt bên AC. Chiết suất của lăng kính bằng:
A. 1,41.
B. 2,0.
C. 1,33.
D. 1,5.
Cho một lăng kính có tiết diện thẳng là một tam giác đều và có chiết suất n =1,5. Chiết một tia tới nằm trong một tiết diện thẳng ABC và vuông góc với mặt bên AB của lăng kính
Tia sáng sẽ
A. ló ra ở mặt bên AC
B. ló ra ở mặt đáy BC
C. trở lại, ló ra ở mặt AB
D. truyền quanh quẩn bên trong lăng kính và không ló ra ngoài được
Một lăng kính có tiết diện vuông góc là một tam giác đều ABC. Một chùm tia sáng đơn sắc hẹp SI được chiếu tới mặt AB trong mặt phẳng của tiết diện vuông góc và theo phương vuông góc với đường cao AH của ABC. Chùm tia ló khỏi mặt AC theo phương sát với mặt này. Tính chiết suất của lăng kính.
Chiếu một tia sáng đơn sắc, nằm trong tiết diện thẳng, tới mặt bên của một lăng kính có góc chiết quang A (như hình vẽ). Tia ló ra khỏi mặt bên và đối xứng với tia tới qua lăng kính. Dùng giác kế (máy đo góc) xác định được A = 60 ° và góc lệch D = 30 ° . Tính: Góc tới i 1 , i 2 và chiết suất n của lăng kính.