Các câu hỏi tương tự
Một khối gỗ hình trụ tròn xoay có bán kính đáy bằng 1, chiều cao bằng 2. Người ta khoét từ hai đầu khối gỗ hai nửa khối cầu mà đường tròn đáy của khối gỗ là đường tròn lớn của mỗi nửa khối cầu. Tỉ số thể tích phần còn lại của khối gỗ và cả khối gỗ ban đầu là A. 2/3 B. 1/4 C. 1/3 D. 1/2
Đọc tiếp
Một khối gỗ hình trụ tròn xoay có bán kính đáy bằng 1, chiều cao bằng 2. Người ta khoét từ hai đầu khối gỗ hai nửa khối cầu mà đường tròn đáy của khối gỗ là đường tròn lớn của mỗi nửa khối cầu. Tỉ số thể tích phần còn lại của khối gỗ và cả khối gỗ ban đầu là
A. 2/3
B. 1/4
C. 1/3
D. 1/2
Từ một khúc gỗ dạng khối nón tròn xoay có thể tích bằng
343
3
π
c
m
3
và chu vi đường tròn đáy bằng
14
π
c
m
. Trong sản xuất, người ta muốn tạo ra một vật thể có hình dạng khối cầu (S) từ khối gỗ trên. Gọi S là diện tích mặt cầu (S). Tính giá trị lớn nhất của diện tích S A.
196
π
3
−...
Đọc tiếp
Từ một khúc gỗ dạng khối nón tròn xoay có thể tích bằng 343 3 π c m 3 và chu vi đường tròn đáy bằng 14 π c m . Trong sản xuất, người ta muốn tạo ra một vật thể có hình dạng khối cầu (S) từ khối gỗ trên. Gọi S là diện tích mặt cầu (S). Tính giá trị lớn nhất của diện tích S
A. 196 π 3 − 2 2 c m 2
B. 196 π 6 − 4 2 c m 2
C. 196 π c m 2
D. 196 π 2 c m 2
Có một khối cầu bằng gỗ bán kính R 10cm. Sau khi cưa bằng hai chỏm cầu có bán kính đáy bằng
1
2
R
đối xứng nhau qua tâm của khối cầu, một người thợ mộc đục xuyên tâm của khối cầu gỗ. Người thợ mộc đã đục bỏ đi phần hình hộp chữ nhật có trục của nó trùng với trục hình cầu và có hai mặt lần lượt nằm trên hai mặt phẳng chứa hai đáy của chỏm cầu; hai mặt này là hai hình vuông có đường chéo bằng R (tham khảo hình vẽ bên). Tính thể tích V của phần...
Đọc tiếp
Có một khối cầu bằng gỗ bán kính R = 10cm. Sau khi cưa bằng hai chỏm cầu có bán kính đáy bằng 1 2 R đối xứng nhau qua tâm của khối cầu, một người thợ mộc đục xuyên tâm của khối cầu gỗ. Người thợ mộc đã đục bỏ đi phần hình hộp chữ nhật có trục của nó trùng với trục hình cầu và có hai mặt lần lượt nằm trên hai mặt phẳng chứa hai đáy của chỏm cầu; hai mặt này là hai hình vuông có đường chéo bằng R (tham khảo hình vẽ bên).
Tính thể tích V của phần còn lại của khối cầu (làm tròn đến chữ số thập phân thứ ba)

A. V = 3215 , 023 c m 3 .
B. V = 3322 , 765 c m 3 .
C. V = 3268 , 894 c m 3 .
D. V = 3161 , 152 c m 3 .
Một khối gỗ hình trụ với bán kính đáy bằng 6 và chiều cao bằng 8. Trên một đường tròn đáy nào đó ta lấy hai điểm A,B sao cho cung
A
B
có số đo
120
°
. Người ta cắt khúc gỗ bởi một mặt phẳng đi qua A, B và tâm của hình trụ (tâm của hình trụ là trung điểm của đoạn nối tâm hai đáy) để được thiết diện như hình vẽ. Tính diện tích S của thiết diện thu được. A. S 20
π
+30
3
B. S 20
π
+...
Đọc tiếp
Một khối gỗ hình trụ với bán kính đáy bằng 6 và chiều cao bằng 8. Trên một đường tròn đáy nào đó ta lấy hai điểm A,B sao cho cung A B có số đo 120 ° . Người ta cắt khúc gỗ bởi một mặt phẳng đi qua A, B và tâm của hình trụ (tâm của hình trụ là trung điểm của đoạn nối tâm hai đáy) để được thiết diện như hình vẽ. Tính diện tích S của thiết diện thu được.
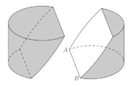
A. S = 20 π +30 3
B. S = 20 π +25 3
C. S = 12 π +18 3
D. S = 20 π
Một khối gỗ có dạng hình nón như hình vẽ, chiều cao của khối gỗ là 10cm đáy khối gỗ là hình tròn có bán kính 4cm Để tạo nên cục chặn giấy có dạng hình chóp tứ giác đều, bác thợ mộc phải đục khối gỗ thành khối chóp tứ giác đều sao cho khối chóp đó có thể tích lớn nhất. Biết rằng khối gỗ ban đầu có khối lượng riêng là
0
,
9
g
a
m
/
c
m
3
Khối lượng cục chặn giấy được tạo thành có...
Đọc tiếp
Một khối gỗ có dạng hình nón như hình vẽ, chiều cao của khối gỗ là 10cm đáy khối gỗ là hình tròn có bán kính 4cm Để tạo nên cục chặn giấy có dạng hình chóp tứ giác đều, bác thợ mộc phải đục khối gỗ thành khối chóp tứ giác đều sao cho khối chóp đó có thể tích lớn nhất. Biết rằng khối gỗ ban đầu có khối lượng riêng là 0 , 9 g a m / c m 3 Khối lượng cục chặn giấy được tạo thành có giá trị gần nhất với giá trị nào sau đây?
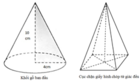
A. m=96gam
B. m=111gam
C. m=90gam
D. m=133gam
Một khối hình trụ có chiều cao bằng 3 lần đường kính của mặt đáy chứa đầy nước. Người ta đặt vào trong khối đó một khối cầu có đường kính bằng đường kính khối trụ và một khối nón có đỉnh tiếp xúc với khối cầu, đáy khối nón trùng với đáy trên của khối trụ (như hình vẽ). Tính tỉ số thể tích của lượng nước còn lại trong khối trụ và lượng nước của khối trụ ban đầu. A.
4
9
B.
5
9
C.
2...
Đọc tiếp
Một khối hình trụ có chiều cao bằng 3 lần đường kính của mặt đáy chứa đầy nước. Người ta đặt vào trong khối đó một khối cầu có đường kính bằng đường kính khối trụ và một khối nón có đỉnh tiếp xúc với khối cầu, đáy khối nón trùng với đáy trên của khối trụ (như hình vẽ).
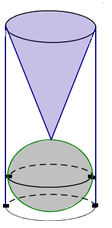
Tính tỉ số thể tích của lượng nước còn lại trong khối trụ và lượng nước của khối trụ ban đầu.
A. 4 9
B. 5 9
C. 2 3
D. 1 2
Có một bể hình hộp chữ nhật chứa đầy nước. Người ta cho ba khối nón giống nhau có thiết diện qua trục là một tam giác vuông cân vào bể sao cho ba đường tròn đáy của ba khối nón tiếp xúc với nhau, một khối nón có đường tròn đáy chỉ tiếp xúc với một cạnh của đáy bể và hai khối nón còn lại có đường tròn đáy tiếp xúc với hai cạnh của đáy bể. Sau đó người ta đặt lên đỉnh của ba khối nón một khối cầu có bán kính bằng 4/3 lần bán kính đáy của khối nón. Biết khối cầu vừa đủ ngập trong nước và lượng nước...
Đọc tiếp
Có một bể hình hộp chữ nhật chứa đầy nước. Người ta cho ba khối nón giống nhau có thiết diện qua trục là một tam giác vuông cân vào bể sao cho ba đường tròn đáy của ba khối nón tiếp xúc với nhau, một khối nón có đường tròn đáy chỉ tiếp xúc với một cạnh của đáy bể và hai khối nón còn lại có đường tròn đáy tiếp xúc với hai cạnh của đáy bể. Sau đó người ta đặt lên đỉnh của ba khối nón một khối cầu có bán kính bằng 4/3 lần bán kính đáy của khối nón. Biết khối cầu vừa đủ ngập trong nước và lượng nước trào ra là 337 π 3 c m 3 . Tính thể tích nước ban đầu ở trong bể
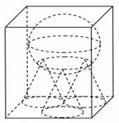
A. ≈ 885 , 2 c m 3
B. ≈ 1209 , 2 c m 3
C. ≈ 1106 , 2 c m 3
D. ≈ 1174 , 2 c m 3
Một khối gỗ hình trụ đường kính 0,5m và chiều cao 1m. Người ta đã cắt khối gỗ, phần còn lại như hình vẽ bên có thể tích là V. Tính V? A.
3
π
16
m
3
B.
5
π
64
m
3
C.
3
π
64
m
3...
Đọc tiếp
Một khối gỗ hình trụ đường kính 0,5m và chiều cao 1m. Người ta đã cắt khối gỗ, phần còn lại như hình vẽ bên có thể tích là V. Tính V?
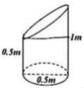
A. 3 π 16 m 3
B. 5 π 64 m 3
C. 3 π 64 m 3
D. π 16 m 3
Một khúc gỗ có dạng khối nón có bán kính đáy r 30 km, chiều cao h 120 km. Anh thợ mộc chế tác khúc gỗ đó thành một khúc gỗ có dạng khối trụ như hình vẽ. Gọi V là thể tích lớn nhất của khúc gỗ dạng khối trụ có thể chế tác được. Tính V A.
V
0
,
16
m
3
B.
V
0
,
024
m
3
C.
V...
Đọc tiếp
Một khúc gỗ có dạng khối nón có bán kính đáy r= 30 km, chiều cao h= 120 km. Anh thợ mộc chế tác khúc gỗ đó thành một khúc gỗ có dạng khối trụ như hình vẽ. Gọi V là thể tích lớn nhất của khúc gỗ dạng khối trụ có thể chế tác được. Tính V
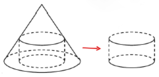
A. V = 0 , 16 m 3
B. V = 0 , 024 m 3
C. V = 0 , 027 m 3
D. V = 0 , 016 m 3




