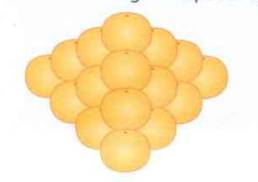
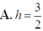Một cửa hàng có 100 quả cam, một người muốn xếp 100 quả cam thành một tứ diện có 4 mặt, mỗi mặt là hình tam giác và đáy là hình vuông (như hình vẽ).
Biết số quả cam trong khối tứ diện bốn mặt với n lớp được tính theo công thức \(\dfrac{1}{6}n\left(n+1\right)\left(n+2\right)\). Tính số lớp tối đa người này có thể xếp 100 quả cam thành hình tứ diện như trên.
Ta sử dụng phương pháp thử và sai, bắt đầu với n = 1 và tăng giá trị của n cho đến khi 1/6n(n+1)(n+2) vượt quá 100. Khi đó, n - 1 sẽ là số lớp tối đa của khối tứ diện.
Thử nghiệm:
- Với n = 1: 1/6 x 1 x 2 x 3 = 1, không vượt quá 100.
- Với n = 2: 1/6 x 2 x 3 x 4 = 4, không vượt quá 100.
- Với n = 3: 1/6 x 3 x 4 x 5 = 10, không vượt quá 100.
- Với n = 4: 1/6 x 4 x 5 x 6 = 20/3, vượt quá 100.
Vậy, số lớp tối đa của khối tứ diện được xếp từ 100 quả cam là n - 1 = 3.