\(n\left(\Omega\right)=C^4_{15}\)
\(n\left(A\right)=C^4_4+C^1_6\cdot C^1_5\cdot C^2_4+C^2_6\cdot C^2_5=331\)
=>p(A)=331/1365
\(n\left(\Omega\right)=C^4_{15}\)
\(n\left(A\right)=C^4_4+C^1_6\cdot C^1_5\cdot C^2_4+C^2_6\cdot C^2_5=331\)
=>p(A)=331/1365
Một hộp đựng 15 viên bị khác nhau gồm 4 bi đỏ, 5 bi trắng và 6 bi vàng. Tính số cách chọn 4 viên bi từ hộp đó sao cho không có đủ 3 màu
A. 465
B. 456
C. 654
D. 645
Mình cần gấp ạ
Bài 2: Một bình đựng 5 viên bi đỏ, 6 viên bi trắng và 7 viên bi vàng. Lấy ngẫu nhiên 4 viên bi. Tính xác suất các biến cố sau:
a) 4 viên bi được chọn có đúng 1 viên màu đỏ
b) 4 viên bi được chọn có ít nhất 2 viên bi vàng
Một chiếc hộp đựng 5 viên bi trắng, 3 viên bi xanh và 4 viên bi vàng. Lấy ngẫu nhiên 4 viên bi từ hộp đó. Tính xác suất để lấy ra 4 viên bi có đủ ba màu.
A . 4 11
B . 5 11
C . 3 11
D . 6 11
Một hộp đựng 40 viên bi trong đó có 20 viên bi đỏ, 10 viên bi xanh, 6 viên bi vàng,4 viên bi trắng. Lấy ngẫu nhiên 2 bi, tính xác suất biến cố A: “ lấy được 2 viên bi cùng màu”.
A. 4 195
B. 6 195
C. 4 15
D. 64 195
Trong một chiếc hộp có 6 viên bi đỏ, 5 viên bi vàng và 4 viên bi trắng. Lấy ngẫu nhiên trong hộp ra 4 viên bi. Xác suất để trong 4 viên bi lấy ra không có đủ cả ba màu
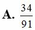
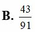
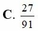
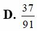
Một bình chứa 16 viên bi với 7 viên bi trắng, 6 viên bi đen và 3 viên bi đỏ. Lấy ngẫu nhiên 3 viên bi. Lấy ngẫu nhiên 3 viên bi. Tính xác suất lấy được cả 1 viên bi trắng, 1 viên bi đen, 1 viên bi đỏ.
A. 1/560
B. 9/40
C. 1/28
D. 143/280
Một hộp đựng 40 viên bi trong đó có 20 viên bi đỏ, 10 viên bi xanh, 6 viên bi vàng,4 viên bi trắng. Lấy ngẫu nhiên 2 bi, tính xác suất biến cố :
A: “2 viên bi cùng màu”.
A. 64/145
B. 64/195
C. 64/185
D. 64/175
Một bình chứa 16 viên bi, với 7 viên bi trắng, 6 viên bi đen, 3 viên bi đỏ. Lấy ngẫu nhiên 3 viên bi. Tính xác suất lấy được 1 viên bi trắng, 1 viên bi đen, 1 viên bi đỏ.
A. 1 210 .
B. 3 80 .
C. 9 40 .
D. 1 35 .
Một hộp có 5 bi xanh và 7 bi đỏ. Cứ thực hiện lấy ngẫu nhiên ra 1 viên rồi bỏ lại vào hộp. Hỏi phải lấy ngẫu nhiên ít nhất bao nhiêu lần để xác suất lấy được 1 viên bị đỏ lớn hơn hoặc bằng 0,9.
![]()
![]()
![]()
![]()