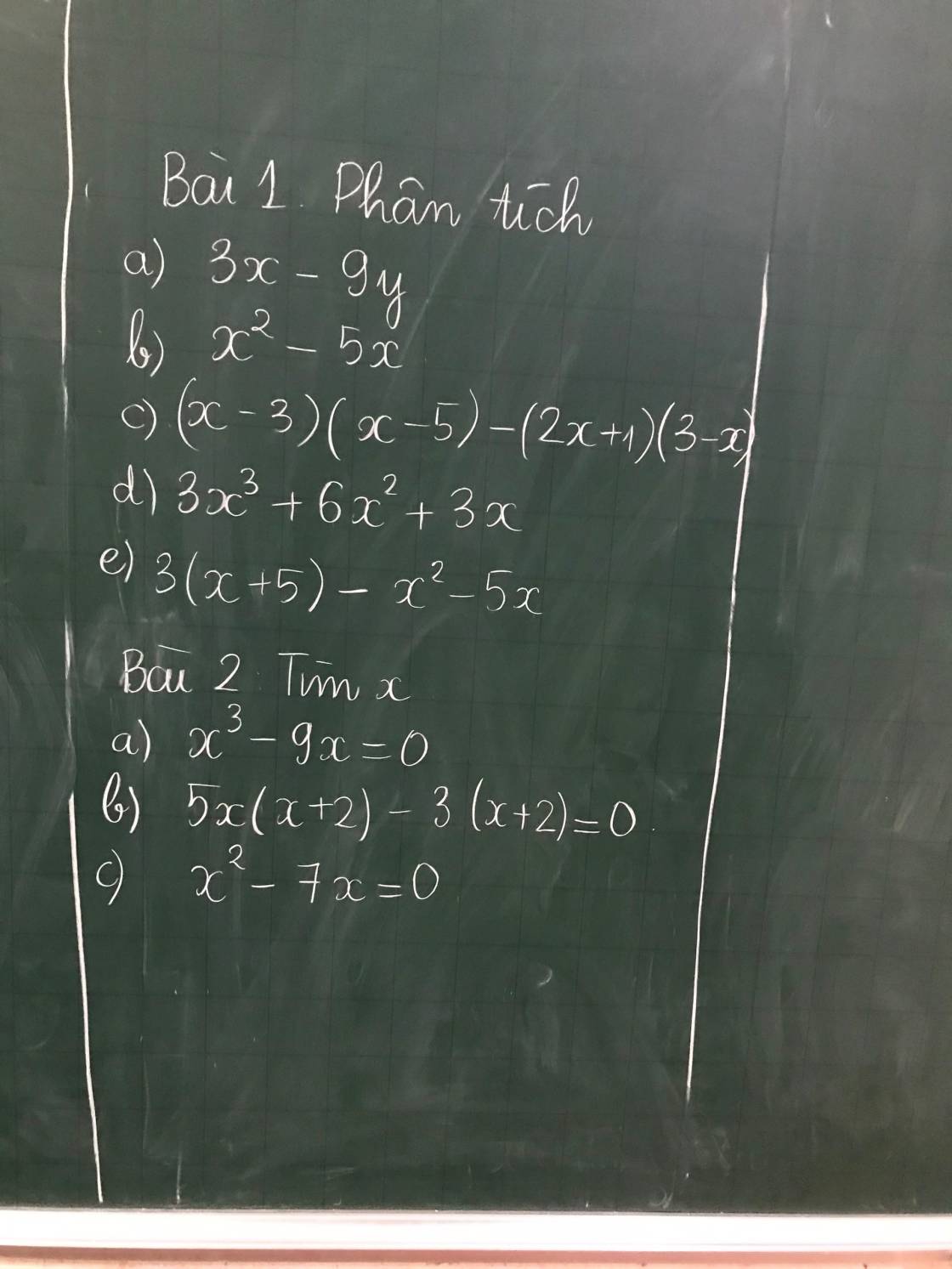\(a,b>0\)
\(a+b=1\Leftrightarrow\left(a+b\right)^2=1\)
-Áp dụng BĐT AM-GM ta có:
\(\left(a+b\right)^2\ge4ab\Rightarrow1^2\ge4ab\Leftrightarrow ab\le\dfrac{1}{4}\)
\(P=a^3+b^3+\dfrac{4}{ab}-ab=\left(a+b\right)\left(a^2-ab+b^2\right)+\dfrac{4}{ab}-ab=a^2-ab+b^2+\dfrac{4}{ab}-ab=\left(a-b\right)^2+\dfrac{4}{ab}\ge0+\dfrac{4}{\dfrac{1}{4}}=16\)\(P_{min}=16\Leftrightarrow a=b=\dfrac{1}{2}\)






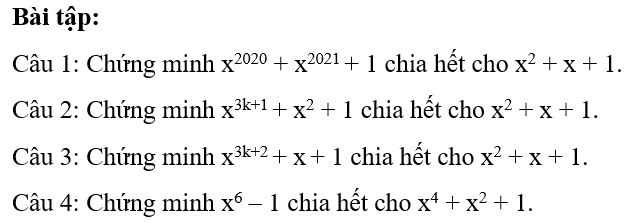




 em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp
em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp