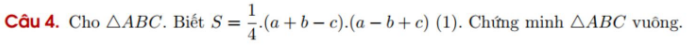Ta có: `a.b = 0`
`=>` \(\left[ \begin{array}{l}a= 0 \\b=0\end{array} \right.\)
`+) A xx B = cancel O`
`=>` \(\left[ \begin{array}{l}A= ∅ \\B=∅\end{array} \right.\) ( dpcm)`.
Ta có : \(a\times b=0\)
Vậy :
\(\Rightarrow\left[\dfrac{a=0}{b=0}\right]\)
\(\Rightarrow A\times B=\varnothing\)
\(\Rightarrow\left[\dfrac{A=\varnothing}{B=\varnothing}\right]\left(đpcm\right)\)
2 bạn dưới trả lời, thực chất chưa hiểu rõ về khái niệm tích Decartes của 2 tập hợp, mời đọc lại trên Wikipedia.
Bài này mình sẽ chứng minh bằng phản chứng. Thật vậy, giả sử A, B đều không phải tập rỗng.
Khi đó, tồn tại \(x \in A\)và \(y\in B\). Khi này \((x;y) \in \) A x B
Tức là A x B khác \(\varnothing\) (trái giả thiết).
Vậy giả sử sai, ta có điều phải chứng minh.

 .
.