\(a+b=1\)
=>a=1-b
\(\dfrac{a}{b^3-1}+\dfrac{b}{a^3-1}=\dfrac{1-b}{\left(b-1\right)\left(b^2+b+1\right)}+\dfrac{b}{\left(1-b\right)^3-1}\)
\(=\dfrac{-1}{b^2+b+1}+\dfrac{b}{\left(1-b-1\right)\left[\left(1-b\right)^2+1\left(1-b\right)+1\right]}\)
\(=\dfrac{-1}{b^2+b+1}+\dfrac{-1}{b^2-2b+1+1-b+1}\)
\(=\dfrac{-1}{b^2+b+1}+\dfrac{-1}{b^2-3b+3}=\dfrac{-b^2+3b-3-b^2-b-1}{\left(b^2+b+1\right)\left(b^2-3b+3\right)}\)
\(=\dfrac{-2b^2+2b-4}{\left(b^2+b+1\right)\left(b^2-3b+3\right)}\)
\(=\dfrac{-2b^2+2b-4}{b^4-3b^3+3b^2+b^3-3b^2+3b+b^2-3b+3}\)
\(=\dfrac{-2b^2+2b-4}{b^4-2b^3+b^2+3}\)(2)
\(\dfrac{2\left(ab-2\right)}{a^2b^2+3}\)
\(=\dfrac{2\left[b\left(1-b\right)-2\right]}{\left(1-b\right)^2b^2+3}=\dfrac{2\left[b-b^2-2\right]}{\left(b-b^2\right)^2+3}\)
\(=\dfrac{-2b^2+2b-4}{b^4-2b^3+b^2+3}\)(1)
Từ (1),(2) suy ra \(\dfrac{a}{b^3-1}+\dfrac{b}{a^3-1}=\dfrac{2\left(ab-2\right)}{a^2b^2+3}\)














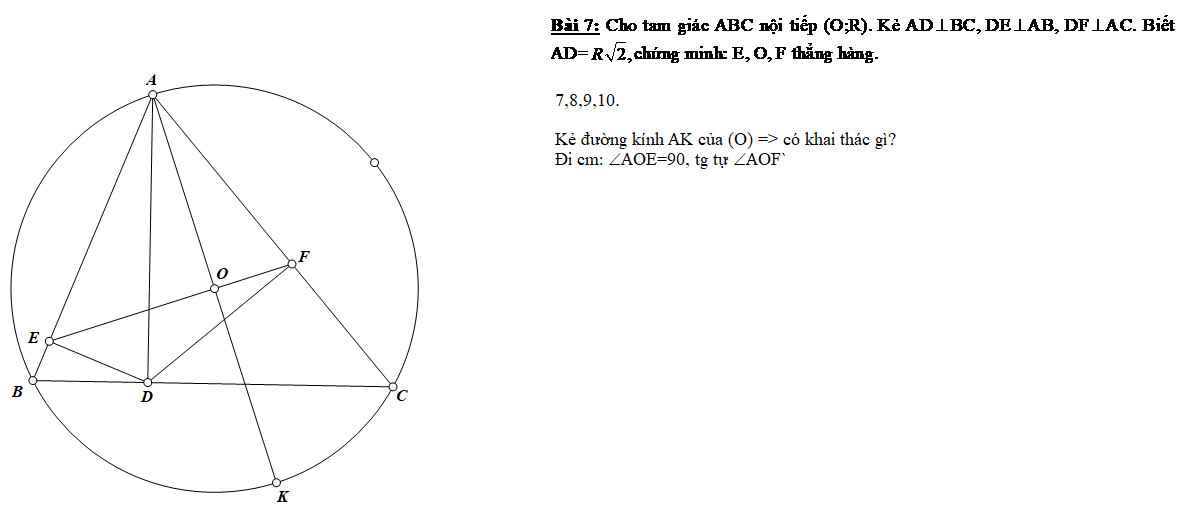



 em cần giải gấp bài 2 ạ, mọi người giúp em với ạ
em cần giải gấp bài 2 ạ, mọi người giúp em với ạ




