a, TK: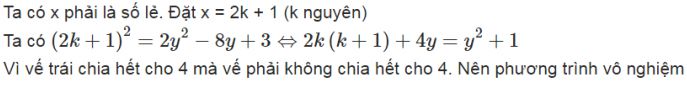
(x lẻ do \(2y^2-8y+3=2\left(y^2-4y\right)+3=x^2\) lẻ)
\(b,\Leftrightarrow\left(x^2-4x+4\right)+\left(y^2+4y+4\right)=9\\ \Leftrightarrow\left(x-2\right)^2+\left(y+2\right)^2=9\)
Vậy pt vô nghiệm do 9 ko phải tổng 2 số chính phương
a, TK: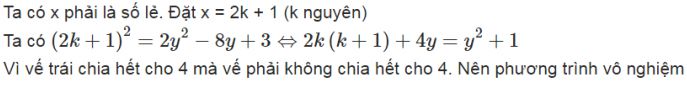
(x lẻ do \(2y^2-8y+3=2\left(y^2-4y\right)+3=x^2\) lẻ)
\(b,\Leftrightarrow\left(x^2-4x+4\right)+\left(y^2+4y+4\right)=9\\ \Leftrightarrow\left(x-2\right)^2+\left(y+2\right)^2=9\)
Vậy pt vô nghiệm do 9 ko phải tổng 2 số chính phương
Giải phương trình nghiệm nguyên
a) \(x^2+6x+17^{91}=2016^{2020}\)
b) \(x^2+2017^{2019}=2016\left(y-1\right)^2\)
c) \(x^2-2x=2017^{2017}\)
d) \(x^2+4x=2018^{10}\)
1. Giải phương trình nghiệm nguyên
a) \(x^2+4x+2018^{10}\)
b) \(x^2+4x+\left(y-1\right)^2=21\)
c) \(x^2+3\left(y-1\right)^2=2021\)
d) \(\left(3x-1\right)^{2020}-18\left(y-2\right)^{2019}=2019^{2020}\)
2. Tìm x,y ∈ Z
a) \(x^2-y^2+6y=56\)
b) \(x^2-4x+9y^2-6y=11\)
Giải phương trình nghiệm nguyên
a) \(3x^2-4y^2=18\)
b) \(19x^2+28y^2=2001\)
c) \(x^2=2y^2-8y+3\)
d) \(x^2+y^2-4x+4y=1\)
\(\sqrt{x-2016}+\sqrt{y-2017}+\sqrt{z-2018}+3024=\frac{1}{2}\left(x+y+z\right)\)
Mấy anh chị giải hộ phương trình này giúp em với. cảm ơn
Giải phương trình nghiệm nguyên
a) 3x^2−4y^2=18
b) 19x^2+28y^2=2001
c) x^2=2y^2−8y+3
d) x^2+y^2-4x+4y=1
Giải phương trình nghiệm nguyên
a) 3x^2−4y^2=18
b) 19x^2+28y^2=2001
c) x^2=2y^2−8y+3
d) x^2+y^2-4x+4y=1
Câu 1. Thực hiện phép chia
\(\left(x^3+x^2-2x+3\right):\left(x+3\right)\)
Câu 2. Phân tích đa thức thành nhân tử
\(x^2-xy-4x+2y+4\)
Câu 3. Cho x, y thỏa mãn \(2x^2+y^2+4=4x+2xy\)
TÍnh giá trị của biểu thức\(A=x^{2016}y^{2017}-x^{2017}y^{2016}+36xy\)
Giải các phương trình sau
a) 22-x(1-4x)=(2x+3)^3
b) 2x/3 + 2x-1/6 = 4- x/3
c) x-1/2019 + x-2/2018 = x-3/2017 + x-4/2016
d) 2-x/2001 - 1 = 1-x/2002 - x/2003
e) 150-x/25 + 188-x/21 + 201-x/19 +171-x/23 =0
Giải phương trình nghiệm nguyên
a) 3x^2−4y^2=18
b) 19x^2+28y^2=2001
c) x^2=2y^2−8y+3
d) x^2+y62−4x+4y=1