Đáp án C.
Hình a,c,d là hình đa diện còn hình b không phải vì nó vi phạm điều kiện, mỗi cạnh chỉ là giao của 2 mặt.
Đáp án C.
Hình a,c,d là hình đa diện còn hình b không phải vì nó vi phạm điều kiện, mỗi cạnh chỉ là giao của 2 mặt.
Cho các hình khối sau:
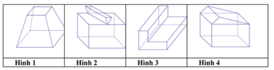
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số đa diện lồi là:
A. 1
B. 2
C. 3
D. 4
Mỗi hình sau gồm một số hữu hạn đa giác phẳng, tìm hình không là hình đa diện
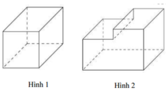
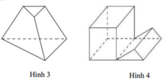
A. Hình 2
B. Hình 4
C. Hình 1
D. Hình 3
Mỗi hình sau gồm một số hữu hạn đa giác phẳng, tìm hình không là hình đa diện.
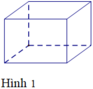
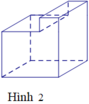
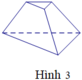
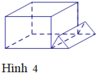
A. Hình 1.
B. Hình 2.
C. Hình 3.
D. Hình 4.
Trên mặt phẳng cho hình 7 cạnh lồi. Xét tất cả các tam giác có đỉnh là các đỉnh của hình đa giác này. Hỏi trong số các tam giác đó, có bao nhiêu tam giác mà cả 3 cạnh của nó đểu không phải là cạnh của hình 7 cạnh đã cho ở trên?
A. 7
B. 9
C. 11
D. 13
Cho các phát biểu sau:
(1). Hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.
(2). Hai đa giác phân biệt của một hình đa diện chỉ có thể có thể hoặc không có điểm chung,
hoặc chỉ có một đỉnh chung, hoặc một cạnh chung.
(3). Mỗi cạnh của đa giác nào của một hình đa diện cũng là cạnh chung của đúng hai đa giác.
Số phát biểu đúng là
A. 0
B. 1
C. 3
D. 2
Cho khối đa diện như hình vẽ bên. Trong đó ABC.A' B' C' là khối lăng trụ tam giác đều có tất cả các cạnh đều bằng 1, S.ABC khối chóp tam giác đều có cạnh bên SA=2/3. Mặt phẳng (SA' B' ) chia khối đa diện đã cho thành hai phần. Gọi V 1 là thể tích phần khối đa diện chứa đỉnh A, V 2 là thể tích phần khối đa diện không chứa đỉnh A. Mệnh đề nào sau đây đúng
A. 72 V 1 = 5 V 2
B. 3 V 1 = V 2
C. 24 V 1 = 5 V 2
D. 4 V 1 = 5 V 2
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, B A D ^ = 60 ° và SA vuông góc với mặt phẳng (ABCD). Góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 450. Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V1, khối đa diện còn lại có thể tích V2 (tham khảo hình vẽ bên). Tính tỉ số V 1 V 2

A. V 1 V 2 = 12 7
B. V 1 V 2 = 5 3
C. V 1 V 2 = 1 5
D. V 1 V 2 = 7 5
Cho khối lập phương ABCD.A’B’C’D’. Cắt khối lập phương trên bởi các mặt phẳng (AB’D’) và (C’BD) ta được ba khối đa diện. Xét các mệnh đề sau:
(I): Ba khối đa diện thu được gồm hai khối chóp tam giác đều và một khối lăng trụ tam giác.
(II): Ba khối đa diện thu được gồm hai khối tứ diện và một khối bát diện đều
(III): Trong ba khối đa diện thu được có hai khối đa diện bằng nhau
Số mệnh đề đúng là:
A. 2
B. 1
C. 3
D. 0
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, và SA vuông góc với mặt phẳng (ABCD). Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng 45 ° . Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V 1 khối đa diện còn lại có thể tích V 2 (tham khảo hình vẽ bên đây). Tính tỉ số V 1 V 2
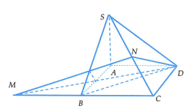
A. V 1 V 2 = 12 7
B. V 1 V 2 = 5 3
C. V 1 V 2 = 1 5
D. V 1 V 2 = 7 5