a: Xét ΔAHM vuông tại M và ΔABH vuông tại H có
\(\widehat{HAM}\) chung
Do đó: ΔAHM đồng dạng với ΔABH
Xét ΔANH vuông tại N và ΔAHC vuông tại H có
\(\widehat{NAH}\) chung
Do đó: ΔANH đồng dạng với ΔABC
b: Ta có: ΔAHM đồng dạng với ΔABH
=>\(\dfrac{AH}{AB}=\dfrac{AM}{AH}\)
=>\(AH^2=AM\cdot AB\left(1\right)\)
Ta có: ΔANH đồng dạng với ΔAHC
=>\(\dfrac{AN}{AH}=\dfrac{AH}{AC}\)
=>\(AH^2=AN\cdot AC\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
c: \(AM\cdot AB=AN\cdot AC\)
=>\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Xét ΔAMN và ΔACB có
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
\(\widehat{MAN}\) chung
Do đó: ΔAMN đồng dạng với ΔACB
Đúng 0
Bình luận (0)
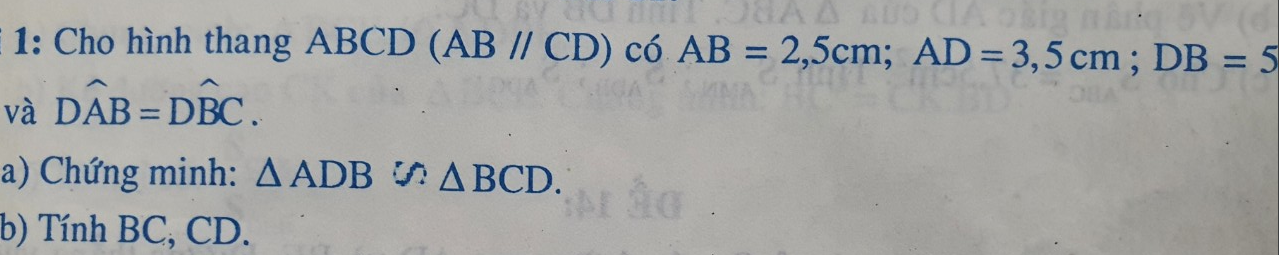
vẽ hình nữa với ạ
