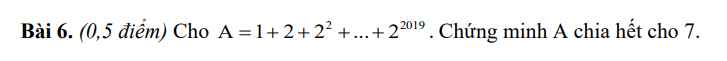\(A=\left(1+2+2^2\right)+\left(2^3+2^4+2^5\right)+...+\left(2^{2017}+2^{2018}+2^{2019}\right)\\ A=\left(1+2+2^2\right)+2^3\left(1+2+2^2\right)+...+2^{2017}\left(1+2+2^2\right)\\ A=\left(1+2+2^2\right)\left(1+2^3+...+2^{2017}\right)\\ A=7\left(1+2^3+...+2^{2017}\right)⋮7\)
\(1+2+2^2+...+2^{2019}\\ =\left(1+2+2^2\right)+\left(2^3+2^4+2^5\right)+...+\left(2^{2017}+2^{2018}+2^{2019}\right)\\ =\left(1+2+2^2\right)+2^3\left(1+2+2^2\right)+...+2^{2017}\left(1+2+2^2\right)\\ =\left(1+2+2^2\right)\left(1+2^3+...+2^{2017}\right)\\ =7\left(1+2^3+...+2^{2017}\right)⋮7\)
A=(1+2+22)+(23+24+25)+...+(22017+22018+22019)A=(1+2+22)+23(1+2+22)+...+22017(1+2+22)
A=(1+2+22)(1+23+...+22017)
A=7(1+23+...+22017)⋮7
=>A\(⋮\)7